当前位置:课程讲解 > 2章 > 8节 > 2点
第八节函数连续性
二、初等函数的连续性
二、初等函数的连续性1.连续函数的四则运算法则[定理1]设函数
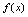 与
与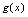 都在点
都在点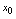 处连续(1)
处连续(1)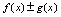 在点
在点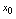 处连续(2)
处连续(2)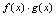 在点
在点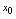 处连续(3)
处连续(3)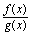 在点
在点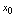 处连续(
处连续( )简言之,连续函数经有限项四则运算所得函数仍是连续函数.[定理2]设函数
)简言之,连续函数经有限项四则运算所得函数仍是连续函数.[定理2]设函数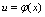 在点
在点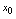 处连续,记
处连续,记 ,而函数
,而函数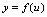 在
在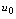 处连续,则复合函数
处连续,则复合函数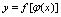 点
点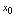 处连续.简言之,连续函数经有限次复合所得函数仍是连续函数.2.基本初等函数的连续性根据定义可证明基本初等函数在有定义的点处连续,即基本初等函数的连续区间就是它的定义域.如
处连续.简言之,连续函数经有限次复合所得函数仍是连续函数.2.基本初等函数的连续性根据定义可证明基本初等函数在有定义的点处连续,即基本初等函数的连续区间就是它的定义域.如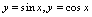 的连续区间就是定义域
的连续区间就是定义域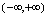 等等.3.初等函数的连续性初等函数是基本初等函数经有限次四则运算或有限次复合所得函数,所以由基本初等函数连续性及四则运算法则可知初等函数在定义域连续.4.函数的间断点<定义2.17>设函数
等等.3.初等函数的连续性初等函数是基本初等函数经有限次四则运算或有限次复合所得函数,所以由基本初等函数连续性及四则运算法则可知初等函数在定义域连续.4.函数的间断点<定义2.17>设函数 在点
在点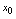 的空心邻域有定义,在点
的空心邻域有定义,在点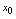 有定义或在点
有定义或在点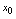 无定义,如果
无定义,如果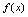 在点
在点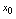 不连续(不满足
不连续(不满足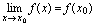 )则称点
)则称点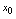 为函数
为函数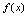 的间断点.例1.单项选择题,设
的间断点.例1.单项选择题,设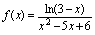 ,
,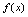 的间断点的个数为( ).A.
的间断点的个数为( ).A.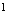 B.
B.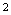 C.
C.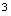 D.无穷多解:应选A.分析:
D.无穷多解:应选A.分析: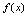 是初等函数,它在定义域连续,故先求出定义域,在定义域内的一个无定义孤立点,就是它的间断点.由
是初等函数,它在定义域连续,故先求出定义域,在定义域内的一个无定义孤立点,就是它的间断点.由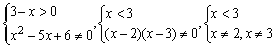 知定义域为
知定义域为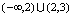 连续,从而
连续,从而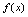 在
在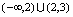 连续,在
连续,在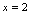 处间断,虽然在
处间断,虽然在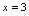 处分母为零,使
处分母为零,使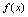 无定义,但它不构成间断点.故只有一个间断点.例2.设
无定义,但它不构成间断点.故只有一个间断点.例2.设 (1)当
(1)当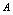 为何值时
为何值时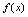 在
在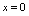 连续(2)当
连续(2)当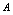 满足什么条件时,
满足什么条件时, 是间断点分析:欲使
是间断点分析:欲使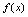 在
在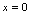 连续,根据定义,应满足
连续,根据定义,应满足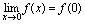 ,而
,而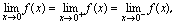 所以实际中,通常用是否有
所以实际中,通常用是否有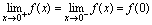 为判定条件.解:(1)
为判定条件.解:(1)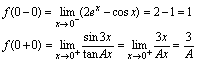 (
(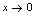 时,
时,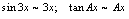 )由
)由 得
得 ,故当
,故当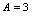 时,
时,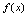 在
在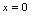 处连续.(2)当
处连续.(2)当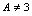 时,
时,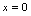 是
是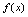 的间断点说明:由(2)知
的间断点说明:由(2)知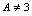 时,
时,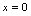 是间断点,如取
是间断点,如取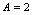 ,有
,有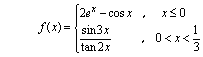 这时,
这时,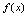 的定义域是
的定义域是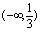 ,而连续区间是
,而连续区间是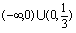 ,这说明初等函数在定义域连续这一结论不能用于分段函数,分段函数可能(只可能)在自变量分段点处不连续.一般而言,在分段函数的自变量分段点处都应该用定义判定连续性.
,这说明初等函数在定义域连续这一结论不能用于分段函数,分段函数可能(只可能)在自变量分段点处不连续.一般而言,在分段函数的自变量分段点处都应该用定义判定连续性.