当前位置:课程讲解 > 2章 > 4节 > 1点
第四节极限的四则运算法则
一、四则法则
一、四则运算法则[定理1]代数和的极限等于极限的代数和.
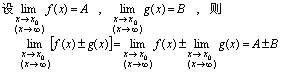 [定理2]乘积的极限等于极限的乘积.
[定理2]乘积的极限等于极限的乘积.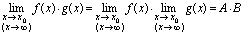 <推论1>常数因子可以提到极限号外
<推论1>常数因子可以提到极限号外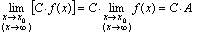 (
(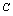 是常数)<推论2>幂的极限等于极限的幂.
是常数)<推论2>幂的极限等于极限的幂.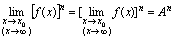 (
(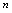 是正整数或正分数)[定理3]当分母的极限不为0时,商的极限等于极限的商.
是正整数或正分数)[定理3]当分母的极限不为0时,商的极限等于极限的商.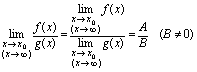 例1.求
例1.求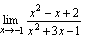 解:
解: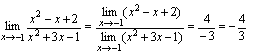 例2.求
例2.求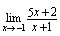 解:
解: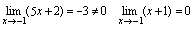 由于不可利用商的定理计算,但有
由于不可利用商的定理计算,但有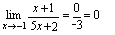 (
(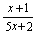 是无穷小量)所以
是无穷小量)所以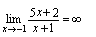 (
(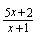 是无穷大量)例3.求
是无穷大量)例3.求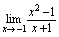 解:
解: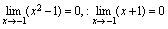 由于不可用商的法则计算
由于不可用商的法则计算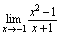 ,同样也不可用商的法则计算
,同样也不可用商的法则计算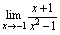 ,实质上,
,实质上,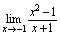 构成
构成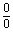 未定式.注意到
未定式.注意到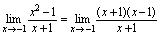 ,而当
,而当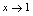 ,但
,但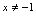 时,
时, ,故可约去分子分母中的公因子
,故可约去分子分母中的公因子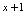 ,从而
,从而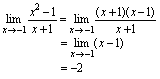 例4.求
例4.求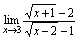
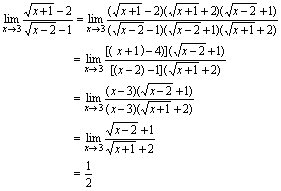 例5.求
例5.求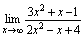 解:分子、分母同除以
解:分子、分母同除以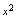
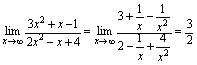 例6.求
例6.求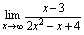 解:
解: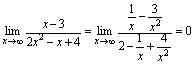 例7.求
例7.求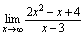 解:
解: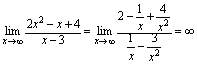 归纳例5,6,7可有如下一般结论:
归纳例5,6,7可有如下一般结论: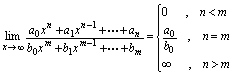 例8.设
例8.设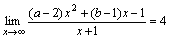 则
则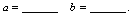 解:由
解:由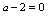 ,知
,知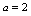 由
由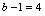 ,知
,知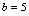 例9.设
例9.设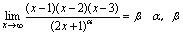 是非零常数,求
是非零常数,求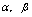 的值.分析:在
的值.分析:在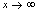 过程中,被求极限是两个多项式之比,有些特征的问题应由上述一般结论为依据求解.解:分子展开后为关于
过程中,被求极限是两个多项式之比,有些特征的问题应由上述一般结论为依据求解.解:分子展开后为关于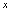 的
的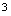 次多项式,已知比的极限为非零常数,故分母应为
次多项式,已知比的极限为非零常数,故分母应为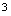 次多项式,所以
次多项式,所以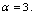 分子、分母为同次多项式条件下,极限应为最高次项系数比,由于分子所含
分子、分母为同次多项式条件下,极限应为最高次项系数比,由于分子所含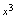 的系数为
的系数为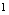 ,分母所含
,分母所含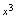 的系数为
的系数为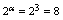 ,所以
,所以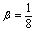 .例10.求
.例10.求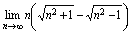 解:
解: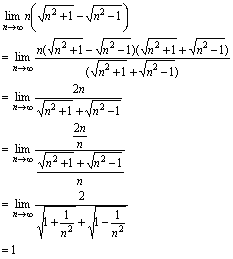 说明:乘有理化因式化为比式后,在
说明:乘有理化因式化为比式后,在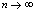 时,类同于例7,8,9的思路,分子,分母除以
时,类同于例7,8,9的思路,分子,分母除以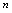 ,化无穷大常数或无穷小.这一方法对含根式的问题亦有效.例11.求
,化无穷大常数或无穷小.这一方法对含根式的问题亦有效.例11.求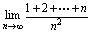 分析:若认为
分析:若认为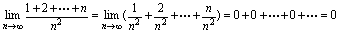 这种想法是错误的.因为在
这种想法是错误的.因为在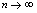 时,分子,分母无穷多项之和,到目前为止,对无穷多项之和并没有建立过运算规则.在无穷多项之和情况下应用有限多项适用的除法分配律是不能认为成立的,正确的思路是:写出
时,分子,分母无穷多项之和,到目前为止,对无穷多项之和并没有建立过运算规则.在无穷多项之和情况下应用有限多项适用的除法分配律是不能认为成立的,正确的思路是:写出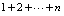 的通式,然后再求极限,通式是:
的通式,然后再求极限,通式是: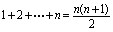 解:
解: