当前位置:课程讲解 > 2章 > 6节 > 1点
第六节无穷小量的比较
一、无穷小量的比较的概念
一、无穷小量比较的概念<定义>设
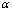 ,
,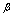 是同一过程中的无穷小量1.若
是同一过程中的无穷小量1.若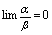 ,则称
,则称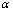 是比
是比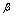 高阶的无穷小量,记为
高阶的无穷小量,记为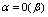 .2.若
.2.若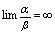 ,则称
,则称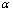 是比
是比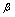 低阶的无穷小量.3.若
低阶的无穷小量.3.若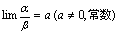 ,则称
,则称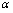 与
与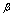 为同阶的无穷小量.4.若
为同阶的无穷小量.4.若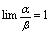 ,则称
,则称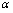 与
与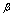 为等价无穷小量,记为
为等价无穷小量,记为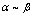 .
.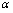 与
与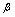 等价,则
等价,则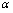 与
与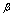 同阶;
同阶;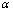 与
与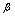 同阶时不一定等价.关于等价无穷小量有下述定理[定理](无穷小量代换定理)设
同阶时不一定等价.关于等价无穷小量有下述定理[定理](无穷小量代换定理)设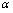 ,
,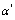 ,
,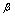 ,
,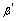 是同过程中的无穷小量,且
是同过程中的无穷小量,且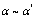 ,
,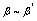 ,则
,则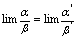 例1.单项选择题当
例1.单项选择题当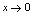 时,
时,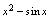 是
是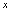 的( ).A.高阶无穷小量B.同阶无穷小量,但不是等价无穷小量C.低阶无穷小量D.等价无穷小量应选B分析:无穷小量的比较的方法,就是求比式的极限,由极限确认两无穷小量的关系.
的( ).A.高阶无穷小量B.同阶无穷小量,但不是等价无穷小量C.低阶无穷小量D.等价无穷小量应选B分析:无穷小量的比较的方法,就是求比式的极限,由极限确认两无穷小量的关系.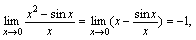 由定义知,当
由定义知,当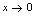 ,
,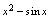 是
是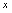 的同阶而非等价无穷小量.例2.求
的同阶而非等价无穷小量.例2.求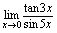 解:此类问题有两种解法<法一>
解:此类问题有两种解法<法一>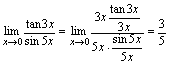 <法二>当
<法二>当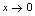 时,
时,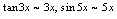
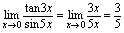 法一是归结为公式,法二是利用等价无穷小代换,相比较法二简单.因此多记一些无穷小量的等价关系,有利于极限的计算.常见等价无穷小量的关系,如下:当
法一是归结为公式,法二是利用等价无穷小代换,相比较法二简单.因此多记一些无穷小量的等价关系,有利于极限的计算.常见等价无穷小量的关系,如下:当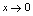 时,
时,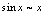 ,
,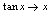 ,
,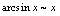 ,
,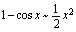 ;
;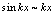 ,
,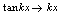 ,
,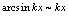 ;
;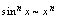 ,
,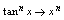 ,
,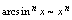 ;
;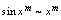 ,
,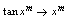 ,
,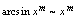 .例3.当
.例3.当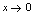 时,无穷小,
时,无穷小,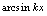 与
与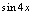 等价,则
等价,则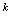 =______.解:填4分析:当
=______.解:填4分析:当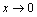 时,
时,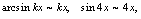 又由已知,有:
又由已知,有: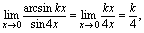 由
由 ,得
,得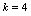 .
.