当前位置:课程讲解 > 2章 > 8节 > 1点
第八节函数连续性
一、函数连续性概念
一、函数连续性1.函数增量<定义2.11>设函数
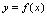 在点
在点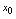 邻域有定义,给自变量
邻域有定义,给自变量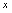 以增量
以增量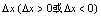 ,称
,称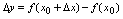 为与
为与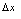 对应的函数增量.由图2-17可知,
对应的函数增量.由图2-17可知,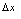 是曲线
是曲线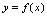 上点
上点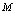 与
与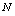 的横坐标之差,
的横坐标之差,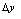 是点
是点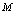 与
与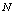 的纵坐标之差.
的纵坐标之差.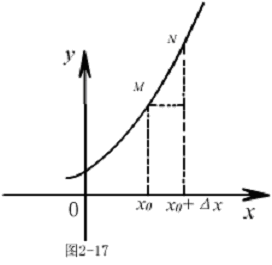 2.函数
2.函数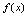 在点
在点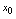 处连续的定义<定义2.12>设
处连续的定义<定义2.12>设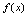 在点
在点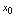 邻域有定义,对应
邻域有定义,对应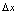 有
有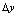 ,如果
,如果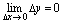 ,则称
,则称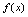 在点
在点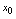 连续,点
连续,点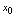 称为
称为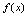 的连续点.在应用中,为了方便,常用如下等价形式的定义.<定义2.13>设
的连续点.在应用中,为了方便,常用如下等价形式的定义.<定义2.13>设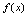 在点
在点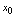 邻域有定义,
邻域有定义,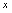 是邻域内一点,如果
是邻域内一点,如果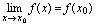 ,则称
,则称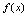 在点
在点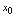 连续.<定义2.14>若
连续.<定义2.14>若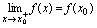 ,则称
,则称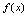 在点
在点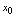 处右连续;若
处右连续;若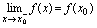 ,则称
,则称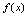 在点
在点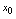 处左连续.由于若
处左连续.由于若 存在的充分必要条件是
存在的充分必要条件是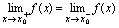 ,所以有:[定理]
,所以有:[定理]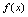 在点
在点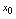 处连续的充分必要条件是
处连续的充分必要条件是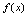 在点
在点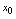 处既右连续也左连续.例1.判明函数
处既右连续也左连续.例1.判明函数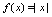 在
在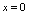 处是否连续解:
处是否连续解: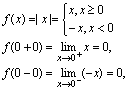 所以,
所以,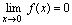 又
又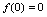 ,从而
,从而 ,故
,故 在
在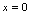 连续.例2.判明函数
连续.例2.判明函数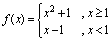 在
在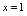 处是否连续解:
处是否连续解: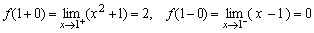 ,由于
,由于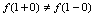 ,从而
,从而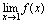 不存在,所以
不存在,所以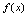 在
在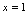 处不连续.(由
处不连续.(由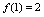 ,
,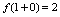 ,可知
,可知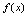 在
在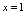 处右连续.又由
处右连续.又由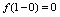 ,可知
,可知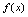 在
在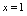 处左不连续)由图2-18看出,曲线
处左不连续)由图2-18看出,曲线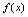 在
在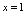 处断开了,即
处断开了,即 不连续.
不连续.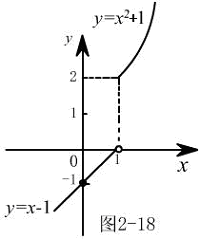 例3.设
例3.设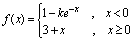 在
在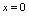 连续,则
连续,则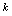 =______.解:应填
=______.解:应填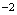 分析:
分析: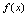 在
在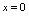 连续的必要条件是
连续的必要条件是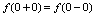 ,由此可解出
,由此可解出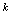 值.
值.  ,
,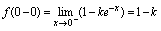 ,由
,由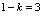 得,
得,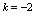 .3.函数
.3.函数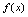 在区间上连续的定义<定义2.15>如果
在区间上连续的定义<定义2.15>如果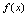 在
在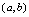 内的每一点都连续,则称
内的每一点都连续,则称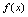 在
在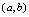 内连续,
内连续, 称为
称为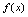 的连续区间.<定义2.16>如果
的连续区间.<定义2.16>如果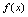 在
在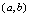 内的每一点都连续,在
内的每一点都连续,在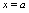 处右连续,在
处右连续,在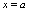 处左连续,则称
处左连续,则称 在
在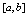 上连续.从几何学角度,若
上连续.从几何学角度,若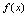 在
在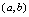 内的每一点都连续,其图形为无缝隙的弧股.
内的每一点都连续,其图形为无缝隙的弧股.