当前位置:课程讲解 > 2章 > 5节 > 1点
第五节两个准则与两个重要极限
一、准则1与重要极限1
一、准则1与重要极限1[准则1]设
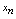 ,
,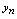 ,
,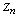 为三个数列,满足1.对一切正整数
为三个数列,满足1.对一切正整数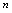 ,
,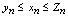 .2.
.2.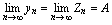 则
则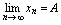 对三个函数,准则1也正确.以准则1为依据,可证出如下重要极限1[重要极限1]
对三个函数,准则1也正确.以准则1为依据,可证出如下重要极限1[重要极限1]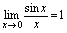 ,更一般地
,更一般地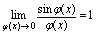 .例1.求
.例1.求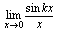 (
(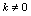 ,常数)分析:含三角函数,必应由重要极限1求解,按公式,
,常数)分析:含三角函数,必应由重要极限1求解,按公式,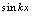 应与
应与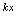 比,所以分子,分母同时乘以
比,所以分子,分母同时乘以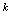 ,且
,且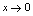 时可保证
时可保证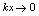 .解:
.解: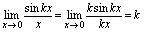 例2.求
例2.求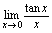 解:
解: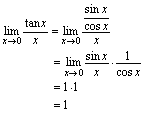 (牢记:
(牢记: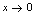 ,
,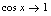 )
)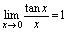 可作为公式使用.例3.求
可作为公式使用.例3.求 分析:应用公式1,根据
分析:应用公式1,根据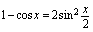 ,化为公式1的形式.解:
,化为公式1的形式.解: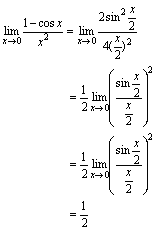 例4.求
例4.求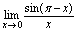 分析:根据三角函数诱导公式
分析:根据三角函数诱导公式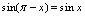 ,化为公式1的形式.解:
,化为公式1的形式.解: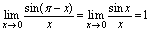 例5.求
例5.求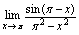 分析:由分式1的更一般形式
分析:由分式1的更一般形式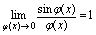 ,将
,将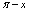 看作
看作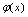 ,注意到当
,注意到当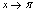 时,
时,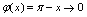 ,
, ,而
,而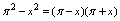 含
含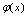 .故可根据公式1求解.解:
.故可根据公式1求解.解: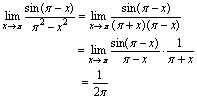 例6.求
例6.求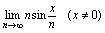 分析:因为
分析:因为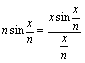 ,当
,当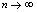 时,
时,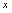 与
与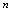 的变化无关的量,可视为常量.从而
的变化无关的量,可视为常量.从而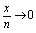 ,故可根据公式1求解.解:
,故可根据公式1求解.解: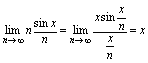 例7.求
例7.求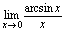 分析:因为
分析:因为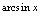 与
与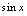 互为反函数,所以应通过反函数变形,化为公式1的形式.解:令
互为反函数,所以应通过反函数变形,化为公式1的形式.解:令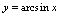 ,则
,则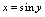 且当
且当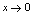 时,
时,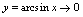 ,从而有
,从而有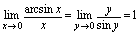 .(由
.(由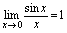 ,易知
,易知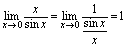 )例8.讨论下述极限
)例8.讨论下述极限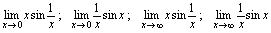 分析:对
分析:对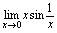 ,当
,当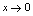 时,
时,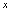 是无穷小.而由于
是无穷小.而由于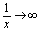 ,
,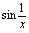 振荡无极限,然而
振荡无极限,然而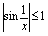 有界,所以根据无穷小运算性质,当
有界,所以根据无穷小运算性质,当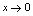 时,
时,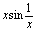 为无穷小乘有界量,仍然是无穷小,故
为无穷小乘有界量,仍然是无穷小,故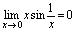 .对
.对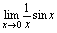 ,因为
,因为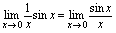 ,它就是重要极限1的形式,因此,由公式知:
,它就是重要极限1的形式,因此,由公式知: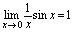 .对
.对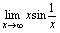 ,注意到
,注意到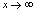 时,
时,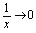 ,再由
,再由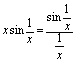 可知它可化为公式1,故由公式有:
可知它可化为公式1,故由公式有: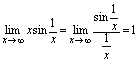 .对
.对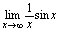 ,当
,当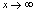 时,
时,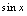 振荡无极限,但
振荡无极限,但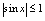 有界,而
有界,而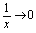 ,于是
,于是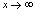 时,
时,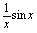 又构成无穷小乘有界量,所以
又构成无穷小乘有界量,所以 .综上,遇到
.综上,遇到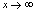 时,
时,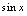 与
与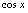 振荡的问题,又含无穷小量因子,则应用无穷小量运算性质,将
振荡的问题,又含无穷小量因子,则应用无穷小量运算性质,将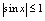 ,
,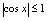 看作有界量;遇到
看作有界量;遇到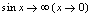 ;
;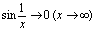 的问题,则应考虑化为重要极限1的形式.
的问题,则应考虑化为重要极限1的形式.