当前位置:课程讲解 > 2章 > 2节 > 1点
第二节函数的极限
一、当x→∞时函数f(x
一、
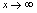 时,函数
时,函数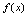 的极限数列是定义在正整数集合上的整标函数,
的极限数列是定义在正整数集合上的整标函数,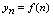 的极限概念是在自变量
的极限概念是在自变量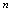 无限增大,即
无限增大,即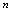 取无限增大的正整数过程中刻划整标函数值
取无限增大的正整数过程中刻划整标函数值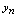 的变化趋势的概念,对于定义在实数集合上的函数
的变化趋势的概念,对于定义在实数集合上的函数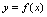 的变化趋势的研究,由于自变量
的变化趋势的研究,由于自变量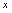 的取值有两种截然不同的状态,即
的取值有两种截然不同的状态,即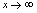 与
与 (
(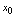 是一个定常数),所以应分别讨论
是一个定常数),所以应分别讨论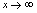 时函数
时函数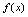 的极限与
的极限与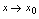 时
时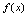 的极限.<定义2.5>给定函数
的极限.<定义2.5>给定函数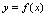 ,在自变量
,在自变量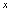 的绝对值
的绝对值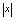 无限增大(记作
无限增大(记作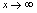 )过程中,对应的函数值趋向于唯一常数
)过程中,对应的函数值趋向于唯一常数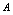 (记作
(记作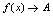 ),则称
),则称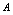 是当
是当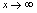 时函数
时函数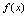 的极限,记作
的极限,记作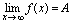 或
或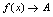 (
(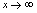 ).例1.讨论函数
).例1.讨论函数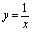 在
在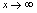 时是否有极限
时是否有极限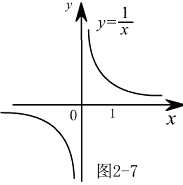 解:观察
解:观察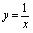 的图形(图2-7),当
的图形(图2-7),当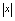 无限增大时,即无论
无限增大时,即无论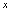 沿横轴向右无限取值还是沿横轴向左无限取值时,对应的函数值愈来愈接近数0,所以当
沿横轴向右无限取值还是沿横轴向左无限取值时,对应的函数值愈来愈接近数0,所以当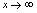 时,函数
时,函数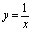 以0为极限,即有
以0为极限,即有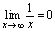 .例2.讨论函数
.例2.讨论函数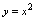 在
在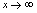 时是否有极限
时是否有极限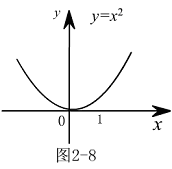 解:观察
解:观察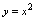 的图形(图2-8),当
的图形(图2-8),当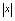 无限增大时,对应的函数值也无限增大,并不趋向于唯一常数,所以,当
无限增大时,对应的函数值也无限增大,并不趋向于唯一常数,所以,当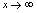 时函数
时函数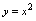 没有极限,形式上可记为
没有极限,形式上可记为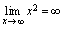 .例3.讨论函数
.例3.讨论函数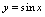 在
在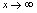 时是否有极限
时是否有极限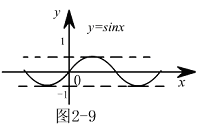 解:观察
解:观察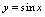 的图形(见2-9),当
的图形(见2-9),当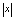 无限增大,函数值
无限增大,函数值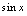 取遍
取遍 上的一切实数值,并不趋向于唯一常数,所以当
上的一切实数值,并不趋向于唯一常数,所以当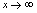 时,函数
时,函数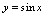 没有极限,这种情况下,称为振荡无极限.如果自变量
没有极限,这种情况下,称为振荡无极限.如果自变量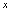 取值从某一时刻以后取正实数,且
取值从某一时刻以后取正实数,且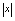 无限增大,则记为
无限增大,则记为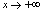 ,即
,即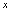 沿
沿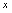 轴向右无限取值,类似的,
轴向右无限取值,类似的,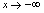 表示
表示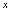 沿
沿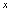 轴向左无限取值.当
轴向左无限取值.当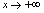 时
时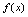 趋向于唯一常数
趋向于唯一常数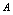 ,则记为
,则记为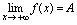 ;当
;当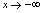 时
时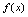 趋向于唯一常数
趋向于唯一常数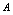 ,则记为
,则记为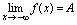 .<命题>
.<命题>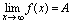 的充分必要条件是
的充分必要条件是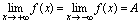 例4.讨论
例4.讨论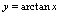 在
在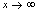 时是否有极限
时是否有极限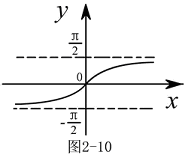 解:观察
解:观察 的图形(图2-10),有
的图形(图2-10),有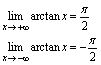 由于
由于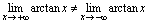 ,所以
,所以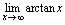 不存在.
不存在.