当前位置:课程讲解 > 2章 > 1节 > 1点
第一节数列的极限
一、数列及性质
一、数列及性质1.数列的概念<定义2.1>定义在正整数集合的函数
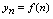 ,当自变量
,当自变量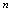 按1,2,3……依次增大取值时,对应的函数值按正整数的顺序排成一串数.
按1,2,3……依次增大取值时,对应的函数值按正整数的顺序排成一串数.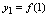 ,
,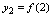 ,……,
,……,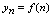 ,……称其为一个无穷数列,简称数列.数列中的每个数称为数列的一项,
,……称其为一个无穷数列,简称数列.数列中的每个数称为数列的一项,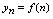 称为一般项.由于在
称为一般项.由于在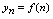 中,自变量
中,自变量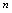 只取正整数,所以通常称
只取正整数,所以通常称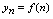 为整标函数.以横轴上的点表示
为整标函数.以横轴上的点表示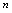 的取值,以
的取值,以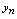 的值为纵坐标,则数列对应坐标平面内自左向右分布的一系列点,称其为数列的图形.将
的值为纵坐标,则数列对应坐标平面内自左向右分布的一系列点,称其为数列的图形.将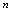 的取值代入一般项
的取值代入一般项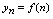 ,则可写出数列的前若干项.例1.设
,则可写出数列的前若干项.例1.设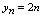 ,
,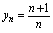 ,
,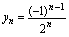 ,
,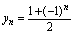 ,
,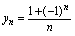 ,
,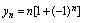 分别写出各数列的前5项.解:
分别写出各数列的前5项.解: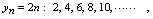 其图形见图2-1
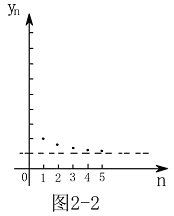
其图形见图2-1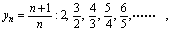 其图形见图2-2
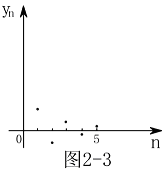
其图形见图2-2 其图形见图2-3
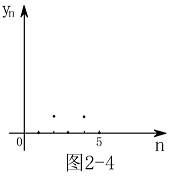
其图形见图2-3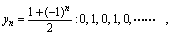 其图形见图2-4
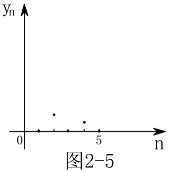
其图形见图2-4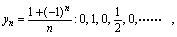 其图形见图2-5
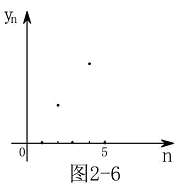
其图形见图2-5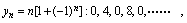 其图形见图2-6
其图形见图2-6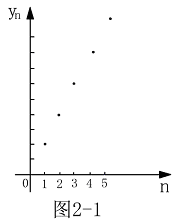
 2.数列的性质<定义2.2>给定数列
2.数列的性质<定义2.2>给定数列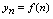 ,若对应一切正整数
,若对应一切正整数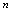 ,有(1)
,有(1)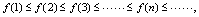 则称为单调增数列;(2)
则称为单调增数列;(2)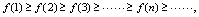 则称为单调减数列;(3)既不满足(1),也不满足(2),则称为摆动数列.<定义2.3>给定数列
则称为单调减数列;(3)既不满足(1),也不满足(2),则称为摆动数列.<定义2.3>给定数列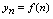 ,若对于一切正整数
,若对于一切正整数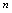 ,存在一个正数
,存在一个正数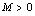 ,使得
,使得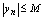 ,则称为有界数列.若使
,则称为有界数列.若使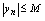 的
的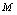 不存在,则称为无界数列.例2.判明例1中各数列的属性解:由写出的各数列的前五项的数值,辅以图形,可知:
不存在,则称为无界数列.例2.判明例1中各数列的属性解:由写出的各数列的前五项的数值,辅以图形,可知: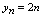 是无界单调增数列.
是无界单调增数列.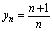 是有界单调减数列.
是有界单调减数列. 是有界摆动数列.
是有界摆动数列.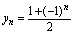 是有界摆动数列.
是有界摆动数列.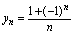 是有界摆动数列.
是有界摆动数列.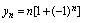 是无界摆动数列.
是无界摆动数列.