当前位置:课程讲解 > 2章 > 1节 > 2点
第一节数列的极限
二、数列的极限
二、数列的极限由例1中各数列的前五项的数值的变化,辅以图形中点的分布状态可以看出,随着项数
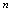 值的逐渐增大,它们有着各自的变化趋势.在项数
值的逐渐增大,它们有着各自的变化趋势.在项数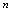 无限增大(通常记为
无限增大(通常记为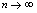 ,“
,“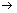 ”理解为“趋向于”)时,可看出:
”理解为“趋向于”)时,可看出: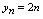 的值无限增大,即
的值无限增大,即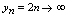
 的值趋向于常数
的值趋向于常数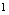 ,即
,即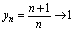
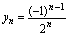 的绝对值趋向于常数
的绝对值趋向于常数 ,即
,即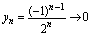
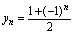 的值当
的值当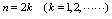 是偶数时趋向于
是偶数时趋向于 ,而当
,而当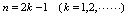 是奇数时趋向于0.
是奇数时趋向于0.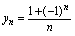 的值趋向于
的值趋向于 ,即
,即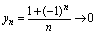
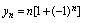 的值当
的值当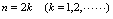 是偶数时无限增大,而当
是偶数时无限增大,而当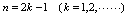 是奇数时趋向于
是奇数时趋向于 .在上述各种变化趋势中,当
.在上述各种变化趋势中,当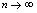 时,如果
时,如果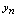 趋向于唯一常数时,我们称数列有极限.<定义2.4>给定数列
趋向于唯一常数时,我们称数列有极限.<定义2.4>给定数列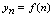 ,在项数
,在项数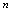 无限增大过程中(记为
无限增大过程中(记为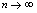 ),如果
),如果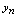 的值趋向于唯一常数
的值趋向于唯一常数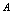 (记为
(记为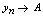 ),则称常数
),则称常数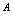 为
为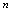 无限增大时数列
无限增大时数列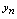 的极限,记作
的极限,记作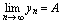 或
或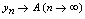 ,亦称
,亦称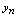 收敛或称
收敛或称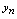 收敛于
收敛于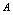 ,否则称
,否则称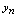 发散,
发散,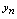 发散时无极限.如前所述
发散时无极限.如前所述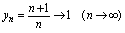 考察
考察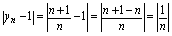 ,当
,当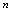 无限增大时,
无限增大时,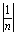 将无限减小,由此可知,
将无限减小,由此可知,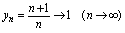 过程中以
过程中以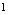 为极限的含义是:对充分大的
为极限的含义是:对充分大的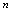 ,
,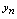 的值与做为它的极限值
的值与做为它的极限值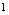 的差的绝对值可以要多小有多小,从图形角度看
的差的绝对值可以要多小有多小,从图形角度看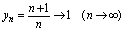 的含义是:当
的含义是:当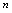 的取值沿
的取值沿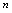 轴向右变化时,对应的点离直线
轴向右变化时,对应的点离直线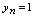 愈来愈接近.根据定义,通过观察,数列
愈来愈接近.根据定义,通过观察,数列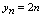 的图形是随
的图形是随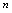 增大沿
增大沿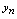 轴正方向愈来愈远离
轴正方向愈来愈远离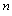 轴的点,即
轴的点,即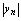 无限增大,所以
无限增大,所以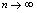 时,
时,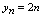 发散无极限,这种情况下,可称为无穷型发散,为表达方式的一致和方便可记为
发散无极限,这种情况下,可称为无穷型发散,为表达方式的一致和方便可记为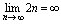 .通过观察,可知在
.通过观察,可知在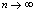 过程中
过程中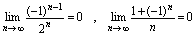 而
而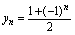 发散(在
发散(在 与
与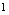 两点跳跃,可称为跳跃型发散),
两点跳跃,可称为跳跃型发散),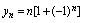 发散(在
发散(在 与无限远点跳跃).
与无限远点跳跃).