第七章 多元函数微积分
学习目的和要求
本章主要学习和了解多元函数的概念，二元函数的几何意义，二元函数的极限和连续性，偏导数和全微分，二元函数可微性、偏导数存在性、连续性之间的关系，复合函数和隐函数的求导法，二阶偏导数，二元函数的极值.二重积分的概念与性质，二重积分的几何意义，二重积分的计算法.
具体要求如下：
1．了解多元函数的概念.
2．理解偏导数的概念.了解全微分的概念.
3．会求二元函数的一阶、二阶偏导数，会求二元函数的全微分.
4．掌握复合函数一阶偏导数的求法.
5．会求由方程
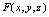所确定的隐函数
的一阶偏导数.6．掌握二元函数极值存在的必要条件.了解二元函数极值存在的充分条件，会求二元函数的极值.
7．了解二重积分的概念与性质，了解二重积分的几何意义，会用二重积分的计算曲顶柱体的体积.
8．掌握在直角坐标系下计算二重积分的方法，会交换积分次序.
9．掌握利用极坐标系计算二重积分的方法. 本章主要内容
第一节 多元函数
一、多元函数概念<定义7.1>设D为一个空的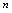
元有序数组
构成的集合，若对于每个
元数组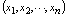
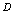，在某个法则
下总有唯一确定的实数
与之对应，则称
为定义在
上的
元函数，记为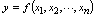
.二、二元函数定义域二元函数
的定义域
是平面区域，即二维数组
构成的平面点的集合.三、二元函数函数值给定二元函数
，当
则对应函数值记为
第二节 二元函数的极限与连续性
一、二元函数的极限<定义7.2>设
在点
的某空心邻域有定义,
为邻域内任意一点，如果当
以任意方式趋近于点
时，
的值趋近于惟一确定常数
，则称
是
当点
趋近于点
时的极限（二重极限）.记作
.二、二元函数在点
处的连续性<定义7.3>设
在点
的领域有定义，如果，
，则
称
在点
处连续.若
在
内每一点都连续，则称
在
连续.类同于一元函数，二元初等函数在定义域连续.
第三节 偏导数与全微分
一、偏导数<定义7.4>设函数
在点
的某个邻域有定义，当
在点
取得增量
，而
不变（应保证点
在此邻域内），如果
存在，称此极限为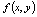
在点
处对自变量
的偏导数.记作
或
或
.同理可定义
二、二阶偏导数如果
，
仍然存在偏导数，则称它们的偏导数为
的二阶偏导数.三、全微分1．概念<定义7.5>设函数
在点
的邻域有定义，自变量
，
分别取得增量
，
，（点
在该邻域内），如果
的全增量
可表示为
.其中
与
无关，
为
时比
高阶的无穷小，则称
在点
处可微，且称
为
在点
处的全微分，记作
2．可微的判定条件3．全微分的求法由定理2可知，求全微分
，应求出两个偏导数
，
，然后写出全微分
.
第四节 复合函数的微分法
一、
型微分法二、
型微分法三、
型微分法
第五节 二元隐函数的微分法
一、隐函数的微分法给定三元方程
，对于
的一组组值，通过方程有唯一确定的
与之对应，可确定二元隐函数
，其两个偏导数的计算公式为：
其中，
，
，
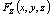分别是三元表达式对
的偏导数，求对一个变量的偏导数时，将另外两个变量暂时看作常量，如：对
求偏导时，将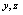
看作常量.
第六节 二元函数极值
一、二元函数极值概念 <定义7.6>设
在点
的邻域有定义，
是邻域内异于
的任意一点.1、如果
为极大值点，
为极大值；2、如果
为极小值点，
为极小值；极大值点与极小值点统称为极值点；极大值与极小值统称为极值.二、二元函数极值存在的判定条件1．必要条件2．充分条件
第七节 二重积分
一、二重积分概念设函数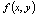
在平面有界闭区域
上有定义，将
分成几个没有公共内点的几个小区域，用
表示第
个小区域及其面积，在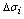
上任取一点
，作和式：
如果极限
存在（其中
表示小区域半径最大者的半径），且其存在性与对
的分法，及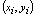
的取法无关，则称此极限为
在
上的二重积分，记作
二、二重积分的性质三、直角坐标系下二重积分的计算四、极坐标系下二重积分的计算