第二章 极限与连续
学习目的和要求
本章主要学习和了解数列极限和函数极限的定义和性质,函数的左极限与右极限,无穷大和无穷小的概念及其关系,无穷小的性质和比较,极限运算法则、极限存在的两个准则(单调有界准则和夹逼准则)两个重要极限:
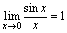
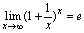 .
.函数连续的概念,左连续与右连续,函数间断点的类型,连续函数的四则运算法则,复合函数的连续性,反函数的连续性,初等函数的连续性,闭区间上连续函数的性质(有界性定理,最大值、最小值定理和介值定理).
具体要求如下:
1.理解数列极限和函数极限的概念.
2.会求数列极限和函数极限(含左极限与右极限)。了解函数在一点处极限存在的充分必要条件.
3.理解无穷小和无穷大的概念.掌握无穷小的性质、无穷小与无穷大的关系.了解高阶、同阶、等价无穷小的概念.会用等价无穷小求极限.
4.会利用极限存在的两个准则求极限.
5.理解函数连续性的概念(含左连续、右连续).会求函数的间断点.
6.掌握连续函数的四则运算法则.
7.理解复合函数、反函数和初等函数的连续性.
8.掌握闭区间上连续函数的性质.
本章主要内容
第一节 数列的极限
一、数列及性质
1.数列的概念
<定义2.1>定义在正整数集全的函数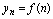 ,当自变量
,当自变量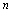 按1,2,3……依次增大取值时,对应的函数值按正整数的顺序排成一串数.
按1,2,3……依次增大取值时,对应的函数值按正整数的顺序排成一串数.
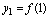 ,
,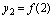 ,……,
,……,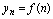 ,……
,……
称其为一个无穷数列,简称数列.
2.数列的性质
<定义2.2>给定数列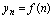 ,若对应一切正整数
,若对应一切正整数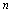 ,有
,有
(1)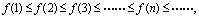 则称为单调增数列;
则称为单调增数列;
(2)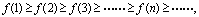 则称为单调减数列;
则称为单调减数列;
(3)即不满足(1),也不满足(2),则称为摆动数列.
<定义2.3>给定数列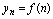 ,若对于一切正整数
,若对于一切正整数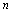 ,存在一个正数
,存在一个正数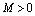 ,使得
,使得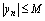 ,则称为有界数列.若使
,则称为有界数列.若使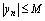 的
的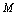 不存在,则称为无界数列.
不存在,则称为无界数列.
二、数列的极限
<定义2.4>给定数列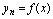 ,在项数
,在项数 无限增大过程中(记为
无限增大过程中(记为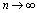 ),如果
),如果 的值趋向于唯一常数
的值趋向于唯一常数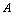 (记为
(记为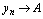 ),则称常数
),则称常数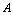 为
为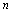 无限增大时数列
无限增大时数列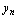 的极限,记作
的极限,记作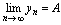 或
或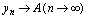 ,亦称
,亦称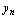 收敛或称
收敛或称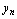 收敛于
收敛于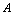 ,否则称
,否则称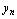 发散,
发散, 发散时无极限.
发散时无极限.
三、数列极限的性质
性质1 (极限存在唯一性)
若数列收敛,则极限为唯一常数.
性质2 收敛数列必为有界数列
应注意,性质2的逆命题不成立,如数列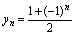 发散,但它有界,这说明有界数列未必收敛.
发散,但它有界,这说明有界数列未必收敛.
性质2的逆命题不成立,但逆否命题一定成立,即,无界数列必发散,如数列 无界,则一定发散.
无界,则一定发散.
第二节 函数的极限
一、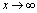 时,函数
时,函数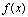 的极限
的极限
<定义2.5>给定函数 ,在自变量
,在自变量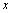 的绝对值
的绝对值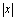 无限增大(记作
无限增大(记作 )过程中,对应的函数值趋向于唯一常数
)过程中,对应的函数值趋向于唯一常数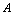 (记作
(记作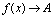 ),则称
),则称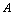 是当
是当 时函数
时函数 的极限,记作
的极限,记作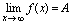 或
或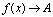 (
( ).
).
二、当 时函数
时函数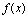 的极限
的极限
<定义2.6>设函数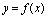 在点
在点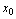 的空心领域
的空心领域 有定义,当自变量
有定义,当自变量 的取值范围趋向于
的取值范围趋向于 时(记作
时(记作 ),对应的函数值
),对应的函数值 趋向于唯一常数
趋向于唯一常数 ,则称常数
,则称常数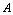 为
为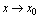 时函数
时函数 的极限,记作
的极限,记作 或
或 .
.
<定义2.7>如果 从点
从点 的左侧(即
的左侧(即 )趋向于
)趋向于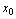 ,称为
,称为 在趋向于
在趋向于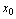 ,记作
,记作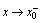 ;如果
;如果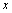 从点
从点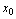 右侧(即
右侧(即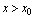 )趋向于
)趋向于 ,称为
,称为 在趋向于
在趋向于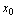 ,记作
,记作 .
.
<定义2.8>若 时,对应函数值
时,对应函数值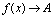 ,则称
,则称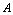 为
为 在点
在点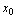 处的左极限,左极限记为
处的左极限,左极限记为 ,即
,即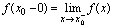 .若
.若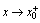 时,对应函数值
时,对应函数值 ,则称
,则称 为
为 在点
在点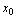 处的右极限,右极限记为
处的右极限,右极限记为 ,即
,即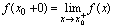 .
.
[定理] 的充分必要条件是
的充分必要条件是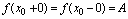 .
.
第三节 无穷小量与无穷大量
一、无穷小量与无穷大量的概念
<定义2.9>以 为极限的变量,称为无穷小量.
为极限的变量,称为无穷小量.
<定义2.10>当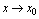 或
或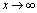 时,
时,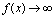 ,则称
,则称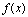 为无穷大量.
为无穷大量.
二、无穷小量与无穷大量的关系
[定理]设 是自变量
是自变量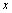 的变化过程(
的变化过程(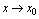 或
或 )中的无穷小量,且
)中的无穷小量,且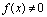 ,则
,则 是同过程中的无穷大量.如果
是同过程中的无穷大量.如果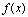 是无穷大量,则
是无穷大量,则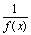 是无穷小量.
是无穷小量.
三、无穷小量的运算性质
[定理1]设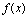 ,
, 是同一过程中的无穷小量,则
是同一过程中的无穷小量,则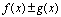 仍是该过程中的无穷小量.
仍是该过程中的无穷小量.
[定理2]设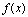 是某过程中的无穷小量,
是某过程中的无穷小量,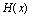 是有界函数,则
是有界函数,则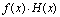 仍是该过程中的无穷小量.
仍是该过程中的无穷小量.
<推论1>常数乘无穷小量仍是无穷小量.
<推论2>有极限的函数乘无穷小量仍是无穷小量.
<推论3>无穷小量乘无穷小量仍是无穷小量.
<推论4>无穷小量的有限次幂仍是无穷小量.
第四节 极限的四则运算法则
一、四则运算法则
[定理1]代数和的极限等于极限的代数和.
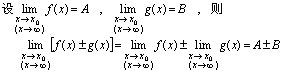
[定理2]乘积的极限等于极限的乘积.

<推论1>常数因子可以提到极限号外
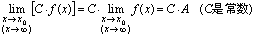
<推论2>幂的极限等于极限的幂.
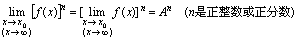
[定理3]当分母的极限膛为0时,商的极限等于极限的商.
第五节 两个准则与两个重要极限
一、准则1与重要极限1
[准则1]设 ,
, ,
, 为三个数列,满足
为三个数列,满足
1.对一切正整数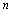 ,
, .
.
2.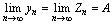
则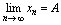
对三个函数,准则1也正确.
以准则1为依据,可证出如下重要极限1
[重要极限1]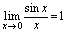 ,更一般地
,更一般地 二、准则2与重要极限2
二、准则2与重要极限2
[准则2]单调有界数列必有极限
以准则2为依据可证重要极限2
[重要极限2]
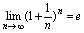
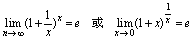
第六节 无穷小量的比较
一、无穷小量比较的概念
<定义>设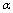 ,
,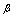 是同一过程中的无穷小量
是同一过程中的无穷小量
1.若 ,则称
,则称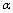 是比
是比 高阶的无穷小量,记为
高阶的无穷小量,记为 .
.
2.若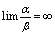 ,则称
,则称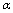 是比
是比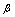 低阶的无穷小量.
低阶的无穷小量.
3.若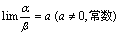 ,则称
,则称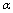 与
与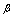 为同阶的无穷小量.
为同阶的无穷小量.
4.若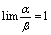 ,则称
,则称 与
与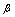 为等阶无穷小量,记为
为等阶无穷小量,记为 .
.
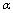 与
与 等价,则
等价,则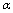 与
与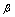 同阶;
同阶;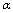 与
与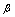 同阶时不一定等价.
同阶时不一定等价.
关于等价无穷小量有下述定理
[定理](无穷小量代换定理)
设 ,
,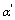 ,
,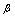 ,
,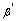 是同过程中的无穷小量,且
是同过程中的无穷小量,且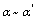 ,
, ,则
,则
常见等价无穷小量的关系,如下:
当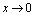 时,
时,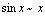 ,
, ,
,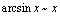 ,
, ;
;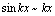 ,
,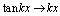 ,
,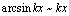 ;
;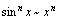 ,
,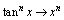 ,
,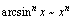 ;
;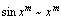 ,
,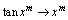 ,
,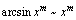
第七节 复合函数的极限
一、复合函数的极限
设当 (或
(或 )时,复合函数
)时,复合函数 有极限,则
有极限,则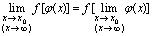 二、含未知参数的极限问题
二、含未知参数的极限问题
1.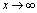 过程的问题
过程的问题
在 过程中,有理分式的极限问题,应依据
过程中,有理分式的极限问题,应依据
 讨论
讨论
2.含无穷小量的问题
3.分段函数问题
第八节 函数连续性
一、函数连续性
1.函数增量
<定义2.11>设函数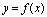 在点
在点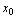 邻域有定义,给自变量
邻域有定义,给自变量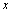 以增量
以增量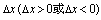 ,称
,称 为与
为与 对应的函数增量.由图2-17可知,
对应的函数增量.由图2-17可知, 是曲线
是曲线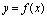 上点
上点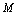 与
与 的横坐标之差,
的横坐标之差,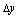 是点
是点 与
与 的纵坐标之差.
的纵坐标之差.
2.函数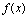 在点
在点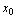 处连续的定义
处连续的定义
<定义2.12>设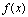 在点
在点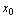 邻域有定义,对应
邻域有定义,对应 有
有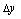 ,如果
,如果 ,则称
,则称 在点
在点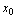 连续,点
连续,点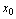 称为
称为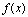 的连续点.
的连续点.
在应用中,为了方便,常用如下等价形式的定义.
<定义2.13>设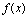 在点
在点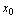 邻域有定义,
邻域有定义,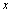 是邻域内一点,如果
是邻域内一点,如果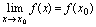 ,则称
,则称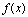 在点
在点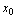 连续.
连续.
<定义2.14>若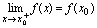 ,则称
,则称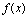 在点
在点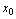 处右连续;若
处右连续;若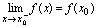 ,则称
,则称 在点
在点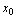 处左连续.
处左连续.
由于若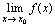 存在的充分必要条件是
存在的充分必要条件是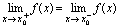 ,所以有:
,所以有:
[定理] 在点
在点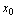 处连续的充分必要条件是
处连续的充分必要条件是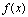 在点
在点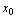 处既右连续也左连续.
处既右连续也左连续.
3.函数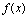 在区间上连续的定义
在区间上连续的定义
<定义2.15>如果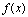 在
在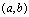 内的每一点都连续,则称
内的每一点都连续,则称 在
在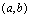 内连续,
内连续,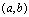 称为
称为 的连续区间.
的连续区间.
<定义2.16>如果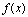 在
在 内的连续,在
内的连续,在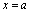 处右连续,在
处右连续,在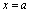 处左连续,则称
处左连续,则称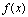 在
在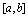 上连续.
上连续.
从几何学角度,若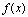 在
在 内连续,其图形为无缝隙的弧股.
内连续,其图形为无缝隙的弧股.
二、初等函数的连续性
1.连续函数的四则运算法则
[定理1]设函数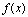 与
与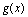 都在点
都在点 处连续
处连续
(1)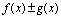 在点
在点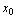 处连续
处连续
(2)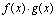 在点
在点 处连续
处连续
(3) 在点
在点 处连续(
处连续(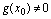 )
)
简言之,连续函数经有限项四则运算所得函数仍是连续函数.
[定理2]设函数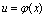 在点
在点 处连续,记
处连续,记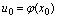 ,而函数
,而函数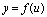 在
在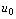 处连续,则复合函数
处连续,则复合函数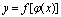 点
点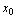 处连续.
处连续.
简言之,连续函数经有限次复合所得函数仍是连续函数.
2.基本初等函数的连续性
根据定义可证明基本初等函数在有定义的点处连续,即基本初等函数的连续区间就是它的定义域.
3.初等函数的连续性
初等函数是基本初等函数经有限次四则运算或有限次复合所得函数,所以由基本初等函数连续性及四则运算法则可知初等函数在定义域连续.
4.函数的间断点
<定义2.17>设函数 在点
在点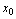 的空心邻域有定义,在点
的空心邻域有定义,在点 有定义或在点
有定义或在点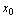 无定义,如果
无定义,如果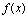 在点
在点 不连续(不满足
不连续(不满足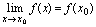 )则称点
)则称点 为函数
为函数 的间断点.
的间断点.
三、闭区间上连续函数的性质
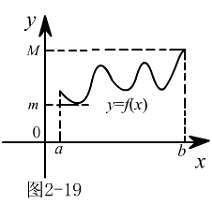
[定理1](最大值与最小值定理)
设 在
在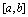 上连续,则
上连续,则 必在
必在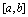 上取得函数值的最大值(通常记为
上取得函数值的最大值(通常记为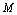 )与函数值的最小值(通常记为
)与函数值的最小值(通常记为 ),取对一切
),取对一切 ,有
,有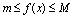 .(参见图2-19)
.(参见图2-19)
[定理2](有界性定理)
设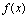 在
在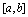 连续,则它在
连续,则它在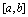 上有界,即存在
上有界,即存在 ,使
,使 ,
,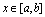 .
.
[定理3](价值性定理)
设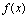 在
在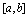 连续,则它在
连续,则它在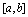 上一定能取到最大值
上一定能取到最大值 与最小值
与最小值 之间的任何一个中间值
之间的任何一个中间值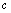 ,即至少存在一个
,即至少存在一个 ,使得
,使得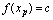 .(参见图2-20)
.(参见图2-20)