第四章 微分中值定理与导数应用
学习目的和要求
本章主要学习和了解微分中值定理(罗尔定理、拉格朗日中值定理),洛必达法则,函数单调性的判别,函数的极值,函数的最大、最小值,函数图形的凹凸性、拐点及渐近线.
具体要求如下:
1.理解并会应用罗尔定理、拉格朗日中值定理
2.熟练掌握用洛必达法则求未定式极限的方法(只要求“
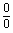 ”、“
”、“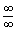 ”、“
”、“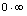 ”、“
”、“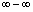 ”型未定式极限)
”型未定式极限)3.掌握利用导数判断函数单调性的方法.
4.理解函数极值的概念.掌握求函数的极值与最大、最小值的方法,并会求解简单的应用问题.
5.会判断平面曲线的凹凸性,会求平面曲线的拐点. 本章主要内容
第一节 微分中值定理
一、罗尔定理如果函数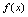 在闭区间
在闭区间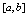 上连续,在开区间
上连续,在开区间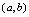 可导,且端点函数值相等,即
可导,且端点函数值相等,即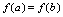 ,则至少存在一点
,则至少存在一点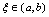 ,使得
,使得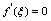 .二、拉格朗日定理如果函数
.二、拉格朗日定理如果函数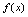 在
在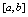 连续,在
连续,在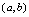 内可导,则至少存在一点
内可导,则至少存在一点 ,使得
,使得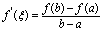 或
或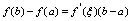 .
.
第二节 洛必达法则
一、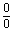 型未定式[定理1]设1.
型未定式[定理1]设1.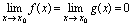 2.在点
2.在点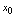 的空心邻域内
的空心邻域内 ,
,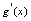 存在,且
存在,且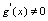 3.
3.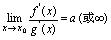 则
则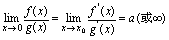 [定理2]设1.
[定理2]设1.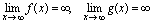 2.对充分大的
2.对充分大的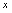 ,
,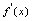 与
与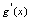 存在,且
存在,且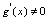 3.
3.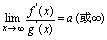 则
则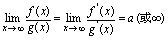 二、
二、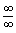 型未定式在定理1与定理2中,将第1个条件中的极限由
型未定式在定理1与定理2中,将第1个条件中的极限由 改为
改为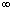 ,则有与两定理同类的结论:
,则有与两定理同类的结论: 三、其他未定式1.
三、其他未定式1.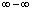 型未定式2.
型未定式2.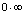 型未定式四、关于洛必达法则的说明洛必达定理的已知条件是充分性质条件,而不是必要性条件.一般而言,遇有振荡函数,则慎用洛必达法则,往往要根据无穷小乘有界量的无穷小未求解.
型未定式四、关于洛必达法则的说明洛必达定理的已知条件是充分性质条件,而不是必要性条件.一般而言,遇有振荡函数,则慎用洛必达法则,往往要根据无穷小乘有界量的无穷小未求解.
第三节 函数单调增减性的判定条件
一、函数单调增减性的判定条件设函数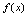 在
在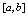 上连续,在
上连续,在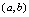 内可导,对任意
内可导,对任意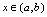 1.如果
1.如果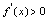 ,则
,则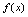 在
在 上单调增加2.如果
上单调增加2.如果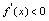 ,则
,则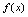 在
在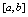 上单调减少
上单调减少
第四节 函数的极值
一、函数的极值的概念<定义4.1>设函数 在点
在点 邻域有定义,
邻域有定义, 为点
为点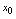 空心邻域内任意一点.1.如果
空心邻域内任意一点.1.如果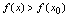 ,则称点
,则称点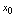 为函数的极小值点,
为函数的极小值点,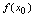 为极小值.2.如果
为极小值.2.如果 ,则称点
,则称点 为函数的极大值点,
为函数的极大值点,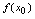 为极大值.极小值与极大值点统称为极值点;极小值与极大值统称为极值.二、极值存在的判定条件1.必要条件[定理1]设点
为极大值.极小值与极大值点统称为极值点;极小值与极大值统称为极值.二、极值存在的判定条件1.必要条件[定理1]设点 是
是 的极值点,
的极值点,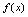 在点
在点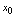 可导,则
可导,则 .2.充分条件[定理2](极值存在的第一充分条件)设
.2.充分条件[定理2](极值存在的第一充分条件)设 是
是 的驻点(即使
的驻点(即使 的点)或使
的点)或使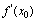 不存在的点.[定理3](极值存在的第二充分条件)设
不存在的点.[定理3](极值存在的第二充分条件)设 是驻点,且
是驻点,且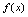 在点
在点 二阶可导1.如果
二阶可导1.如果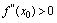 ,则点
,则点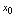 是极小值点.2.如果
是极小值点.2.如果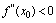 ,则点
,则点 是极大值点.3.如果
是极大值点.3.如果 ,则判定不出极值.三、最大值与最小值由闭区间上连续函数的性质可知,若
,则判定不出极值.三、最大值与最小值由闭区间上连续函数的性质可知,若 在
在 上连续,则必取得最大值
上连续,则必取得最大值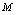 (记为
(记为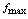 )与最小值
)与最小值 (记为
(记为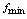 ),
),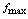 与
与 的求法.
的求法.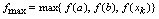
 其中
其中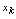 是
是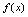 在
在 内的驻点使
内的驻点使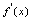 不存在的点.四、最大值与最小值应用问题如果函数在定义域内存在唯一极值,则该极值即为最值(最值是指最大值或最小值),很多刻划实际中的最大,最小值的应用问题的函数都只存在唯一极值,因此,我们可以通过求极值的方法,求解这一类应用问题.
不存在的点.四、最大值与最小值应用问题如果函数在定义域内存在唯一极值,则该极值即为最值(最值是指最大值或最小值),很多刻划实际中的最大,最小值的应用问题的函数都只存在唯一极值,因此,我们可以通过求极值的方法,求解这一类应用问题.
第五节 曲线的凹凸与拐点
一、曲线的凹凸性1.概念<定义>设 在
在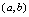 连续,若曲线
连续,若曲线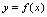 位于其上任意一点处的切线的上方,则称曲线
位于其上任意一点处的切线的上方,则称曲线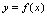 为凹的(图4-4).若曲线
为凹的(图4-4).若曲线 位于其上任意一点处的切线的下方,则称曲线
位于其上任意一点处的切线的下方,则称曲线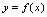 为凸的(图4-5).相应称
为凸的(图4-5).相应称 为
为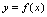 的凹区间和凸区间.2.曲线凹凸性的判定条件[定理]设
的凹区间和凸区间.2.曲线凹凸性的判定条件[定理]设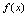 在
在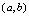 有一阶和二阶导数,对任意
有一阶和二阶导数,对任意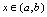 (1)如果
(1)如果 ,则
,则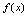 在
在 是凹的(2)如果
是凹的(2)如果 ,则
,则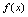 在
在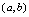 是凸的二、曲线的拐点1.拐点概念若曲线
是凸的二、曲线的拐点1.拐点概念若曲线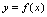 连续,则称曲线凹凸的分界点称为曲线的拐点.2.判定拐点的充分条件是:设点
连续,则称曲线凹凸的分界点称为曲线的拐点.2.判定拐点的充分条件是:设点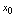 是使
是使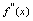 等于零或使
等于零或使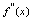 不存在的点.(1)当
不存在的点.(1)当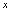 从小于
从小于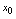 变化到大于
变化到大于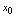 时,
时, 改变符号,则
改变符号,则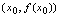 是曲线的拐点.
是曲线的拐点.
(2)当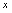 从小于
从小于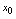 变化到大于
变化到大于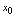 时,
时, 不改变符号,则
不改变符号,则 不是曲线的拐点.
不是曲线的拐点.