第一章 函数
学习目的和要求
本章主要学习和了解函数的定义,函数的表示法,分段函数,反函数,复合函数,隐函数,函数的性质,基本初等函数,初等函数.
具体要求如下:
1.理解函数的概念,掌握函数的表示法,学会求函数的定义域.
2.理解函数的有界性、奇偶性、周期性和单调性.
3.理解分段函数、反函数、复合函数、隐函数
4.掌握基本初等函数的性质和图像,了解初等函数的概念.
本章主要内容
第一节 预备知识
一、绝对值1.绝对值的概念2.有关绝对值的运算性质二、区间区间是指界于某两个实数之间的全体实数,而那两个实数叫做区间的端点.三、邻域与空心邻域设 是常数,
是常数, (希腊字母
(希腊字母 在高等数学中表示绝对值要多小有多小的一个正实数),称满足不等式
在高等数学中表示绝对值要多小有多小的一个正实数),称满足不等式 的实数
的实数 的集合,即以
的集合,即以 为中心的开区间
为中心的开区间 为点
为点 的
的 邻域,通常记作
邻域,通常记作 ,称满足不等式
,称满足不等式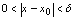 的实数
的实数 的集合,即区间
的集合,即区间 为点
为点 的
的 空心邻域,通常记作
空心邻域,通常记作 .
. 应理解为:实数
应理解为:实数 总是取点
总是取点 附近(要多近有多近)的值,且
附近(要多近有多近)的值,且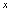 可以等于
可以等于 .
. 应理解为:实数
应理解为:实数 总是取点
总是取点 附近的值,且
附近的值,且 不取
不取 值.
值.
第二节 函数概念
一、函数定义若 是一个非空实数集合,
是一个非空实数集合, 表示某种对应规则,若对每一个
表示某种对应规则,若对每一个 ,在规则
,在规则 总有一个唯一确定的实数
总有一个唯一确定的实数 与之对应,则称对应规则
与之对应,则称对应规则 为定义在
为定义在 上的一个函数关系,或称变量
上的一个函数关系,或称变量 是变量
是变量 的函数,记作
的函数,记作 .
. 称为自变量,
称为自变量, 称为因变量.
称为因变量. 称为函数
称为函数 的定义域,通常记为
的定义域,通常记为 .二、函数表示法函数表示法有解析式法、表格法、图形法.
.二、函数表示法函数表示法有解析式法、表格法、图形法.
第三节 函数的几种简单性质
一、函数的奇偶性给定函数 ,其定义域为
,其定义域为 (
( 不止一个零点)(1)如果对一切
不止一个零点)(1)如果对一切 ,满足
,满足 ,则称
,则称 为偶函数.(2)如果对一切
为偶函数.(2)如果对一切 ,满足
,满足 ,则称
,则称 为奇函数.(3)如果对一切
为奇函数.(3)如果对一切 ,既不满足
,既不满足 ,也不满足
,也不满足 ,则称
,则称 为非奇非偶函数.二、函数的周期性给定函数
为非奇非偶函数.二、函数的周期性给定函数 ,如果存在正数
,如果存在正数 ,使得
,使得 ,则称
,则称 为周期函数,且称使得上式成立的最小的正数
为周期函数,且称使得上式成立的最小的正数 为周期.三、函数的单调性设函数
为周期.三、函数的单调性设函数 在
在 内有定义,任取
内有定义,任取 1.如果
1.如果 ,则称
,则称 在
在 单调增加,简称单调增,区间
单调增加,简称单调增,区间 称为
称为 的单调增区间.2.如果
的单调增区间.2.如果 ,则称
,则称 在
在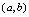 单调减少,简称单调减,区间
单调减少,简称单调减,区间 称为
称为 的单调减区间.四、函数的有界性设函数
的单调减区间.四、函数的有界性设函数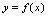 在区间
在区间 有定义,以任意
有定义,以任意 ,如果存在正数
,如果存在正数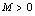 ,使得
,使得 ,则称
,则称 在
在 有界,区间
有界,区间 称为
称为 的有界区间.如果满足上述不等式的
的有界区间.如果满足上述不等式的 不存在,则称
不存在,则称 在
在 无界.
无界.
第四节 反函数、复合函数
一、反函数设 的定义域为
的定义域为 ,值域为
,值域为 .如果对于每一个
.如果对于每一个 都有一个确定的满足
都有一个确定的满足 的
的 与之对应,其对应规则记为
与之对应,其对应规则记为 (读作
(读作 递),这个定义在
递),这个定义在 上的函数
上的函数 称为
称为 的反函数(原型反函数).亦称
的反函数(原型反函数).亦称 与
与 互为反函数.二、复合函数设函数
互为反函数.二、复合函数设函数 ,值域为
,值域为 ,函数
,函数 ,定义域为
,定义域为 ,如果
,如果 与
与 的交集
的交集 不是空集,则称
不是空集,则称 ,是由
,是由 与
与 复合而得的复合函数.
复合而得的复合函数. 是自变量,
是自变量, 是因变量,
是因变量,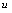 是中间变量.
是中间变量.
第五节 初等函数
基本初等函数中学里学习过的常数函数、幂函数、指数函数、对数函数、三角函数( ,
, ,
, ,
, ,
, ,
, )、反三角函数(
)、反三角函数( ,
, ,
, ,
, )统称为基本初等函数.二、初等函数由基本初等函数经有限次四则运算或有限次复合所得函数统称为初等函数.分段函数不是初等函数.
)统称为基本初等函数.二、初等函数由基本初等函数经有限次四则运算或有限次复合所得函数统称为初等函数.分段函数不是初等函数.