第六章 定积分
学习目的和要求
本章主要学习和了解定积分的概念和基本性质,定积分的几何意义,变上限积分定义的函数及其导数,牛顿-莱布尼茨公式,定积分的换元法和分部积分法,定积分的应用(平面图形的面积、旋转体的体积).
具体要求如下:
1.理解定积分的概念.了解定积分的几何意义.掌握定积分的基本性质.
2.理解变上限积分作为上限的函数的含义,会求这类函数的导数.
3.掌握牛顿-莱布尼茨公式.
4.熟练掌握定积分的换元法和分部积分法.
5.会应用定积分计算平面图形的面积和旋转体的体积. 本章主要内容
第一节 定积分的概念与性质
一、定积分定义<定义6.1>设函数 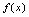 在
在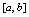 上连续,引入分点
上连续,引入分点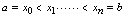 将
将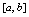 分割为
分割为 个小区间,用
个小区间,用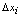 表示第
表示第 个小区间
个小区间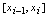 ,且表示其长度,即
,且表示其长度,即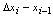 ,记
,记 ,任取点
,任取点 ,若
,若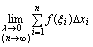 存在,且其值与对
存在,且其值与对 的分法及
的分法及 的选取方法无关,则称
的选取方法无关,则称 在
在 上可积,且称极限为
上可积,且称极限为 在
在 上的定积分,记为
上的定积分,记为 。即
。即
 为积分区间,
为积分区间, 叫积分下限,
叫积分下限, 叫积分上限,
叫积分上限, 叫被积函数,
叫被积函数, 叫被积表达式。二、定积分的性质性质1 定积分具有线性性质2 定积分具有对积分区间的可加性性质3 定积分具有保序性推论1,在
叫被积表达式。二、定积分的性质性质1 定积分具有线性性质2 定积分具有对积分区间的可加性性质3 定积分具有保序性推论1,在 上,
上, ,则
,则 ;
; ,则
,则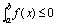 推论2,
推论2, 推论3,在
推论3,在 上
上 连续,存在
连续,存在 ,
, ,从而
,从而 ,则
,则 性质4(定积分中值定理)若
性质4(定积分中值定理)若 在
在 连续,则至少存在一点
连续,则至少存在一点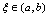 ,使
,使 或
或
第二节 定积分的基本公式
一、变上限函数及其导数1.变上限函数概念设置函数 在
在 上连续,任取x
上连续,任取x ,则
,则 在
在 上亦连续,所以积分
上亦连续,所以积分 存在,(这里将
存在,(这里将 记为
记为 ,是为了避免将被积表达式中的字母
,是为了避免将被积表达式中的字母 与积分上限的
与积分上限的 混淆)。于是对于
混淆)。于是对于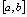 的每个
的每个 ,有唯一确定的积分值
,有唯一确定的积分值 与之对应,称这个函数为上限
与之对应,称这个函数为上限 的变上限函数,记为
的变上限函数,记为 。其定义域为
。其定义域为 。2.变上限函数的导数
。2.变上限函数的导数 变上限函数对上限
变上限函数对上限 的导数等于被积函数在上限的值(即用上限
的导数等于被积函数在上限的值(即用上限 替换
替换 的
的 )由于
)由于 是关于
是关于 的复合函数,由复合函数求导数的链式法则及上限函数导数规则,有
的复合函数,由复合函数求导数的链式法则及上限函数导数规则,有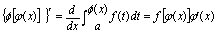 二、牛顿-莱布尼茨公式
二、牛顿-莱布尼茨公式
第三节 定积分的换元法
一、定积分的换元法设函数 在
在 上连续,令
上连续,令 ,如果(1)
,如果(1) 在
在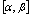 上有连续的导数
上有连续的导数 (2)当
(2)当 从
从 到
到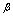 时,
时,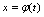 从
从 单调变到
单调变到 则
则 上式从右到左使用,对应不定积分的第一换元积分法;从左到右使用对该不定积分的第二换元积分法。
上式从右到左使用,对应不定积分的第一换元积分法;从左到右使用对该不定积分的第二换元积分法。
第四节 定积分的分部积分法
一、定积分的分部积分法设 ,
,  有连续导数.则
有连续导数.则 这就是定积分的分部积分公式。
这就是定积分的分部积分公式。
第五节 定积分的几何应用
一、平面图形面积的计算二、旋转体的体积的计算