第三章 导数与微分
学习目的和要求
本章主要学习和了解导数和微分的定义,左导数与右导数的几何意义,函数的可导性、可微性与连续性的关系,导数与微分的四则运算法则,导数和微分的基本公式,复合函数。
具体要求如下:
1.理解导数的概念及其几何意义.了解左导数与右导数的概念.
2.了解函数可导性、可微性与连续性的关系.
3.会求平面曲线上一点处的切线方程和法线方程.
4.熟练掌握导数的基本公式、四则运算法则及复合函数的求导方法.
5.会求隐函数的一阶导数.
6.了解高阶导数的概念.会求函数的二阶导数.
7.了解微分的概念.会求函数的微分.
本章主要内容
第一节 导数概念
一、导数定义<定义3.1>设函数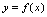 在点
在点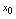 的邻域有定义,对应自变量增量
的邻域有定义,对应自变量增量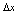 (使
(使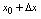 仍在邻域内)有函数增量
仍在邻域内)有函数增量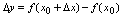 ,如果极限
,如果极限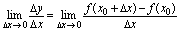 存在,则称
存在,则称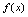 在点
在点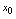 可导,且称存在的极限为
可导,且称存在的极限为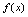 在点
在点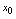 处的导数,记作
处的导数,记作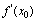 或
或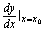 ,
,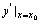 ,即
,即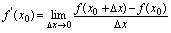 ,如果上述极限不存在,则称
,如果上述极限不存在,则称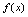 在点
在点 处不可导.若令
处不可导.若令 ,从而
,从而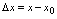 ,且当
,且当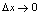 时,
时,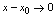 ,
,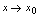 于是有定义1的等价定义.<定义3.2>设
于是有定义1的等价定义.<定义3.2>设 在点
在点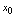 的邻域有定义,
的邻域有定义,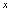 是邻域内一点.如果极限
是邻域内一点.如果极限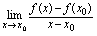 存在,则称
存在,则称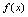 在点
在点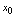 处可导.且称存在的极限为
处可导.且称存在的极限为 的导数,即
的导数,即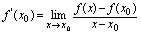 .<定义3.3>若
.<定义3.3>若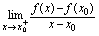 存在,则称此极限为
存在,则称此极限为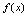 在点
在点 处的右导数,记为
处的右导数,记为 ,即
,即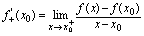 .同理可有左导数
.同理可有左导数 ,即
,即 .由于极限存在的充分必要条件是左、右极限存在且相等,故有如下:[定理]
.由于极限存在的充分必要条件是左、右极限存在且相等,故有如下:[定理]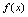 在点
在点 处可导的充分必要条件是左、右导数存在且相等.<定义3.4>若
处可导的充分必要条件是左、右导数存在且相等.<定义3.4>若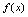 在
在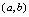 内的每一点都可导,则称
内的每一点都可导,则称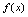 在
在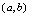 内可导,
内可导,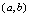 称为
称为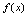 的可导区间.若
的可导区间.若 在
在 内可导,对应每个
内可导,对应每个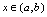 ,都有导数
,都有导数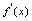 与之对应,所以可称
与之对应,所以可称 为导函数,对取定的一个
为导函数,对取定的一个 ,称
,称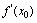 为导数值,显然
为导数值,显然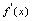 是导函数
是导函数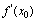 在点
在点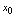 处的函数值,即
处的函数值,即 ,由此,可知
,由此,可知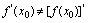 .二、可导性与连续性的关系如果
.二、可导性与连续性的关系如果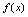 在点
在点 处可导,则
处可导,则 在点
在点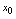 处连续.如果
处连续.如果 在点
在点 连续,但
连续,但 在点
在点 未必可导.如果
未必可导.如果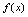 在点
在点 不连续,则
不连续,则 在点
在点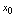 不可导.三、导数的几何意义若
不可导.三、导数的几何意义若 在点
在点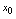 处的导数
处的导数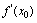 存在,则曲线
存在,则曲线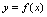 在点
在点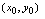 (
(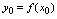 ,
, 称为切点)处有切线,且
称为切点)处有切线,且 为切线的斜率.
为切线的斜率.
第二节 导数运算
一、基本导数公式 (
( 是常数)
是常数) (
(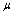 是实数)
是实数)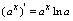 ,
,
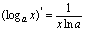 ,
,
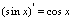
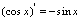

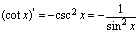

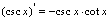

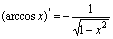

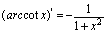 二、复合函数求导法则设
二、复合函数求导法则设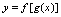 由
由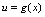 ,
,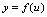 复合而成,若
复合而成,若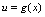 在点
在点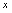 处可导,
处可导, 在
在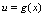 处可导,则
处可导,则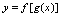 在
在 处可导,且有如下法则:
处可导,且有如下法则: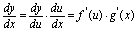 .
.
第三节 高阶导数
一、高阶导数二阶及以上阶导数统称为高阶导数.
第四节 微分
一、微分概念1.微分定义<定义3.4>设 在点
在点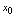 的邻域有定义,
的邻域有定义,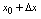 在该邻域内,如果函数增量
在该邻域内,如果函数增量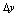 可表为
可表为 ,其中
,其中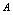 是不依赖
是不依赖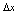 的量,
的量,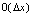 是
是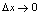 时关于
时关于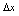 的商阶无穷小量,则称
的商阶无穷小量,则称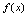 在点
在点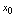 处可微分,简称可微,称
处可微分,简称可微,称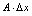 为
为 在点
在点 处的微分,记作
处的微分,记作 ,即
,即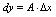 .若
.若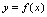 可微,有
可微,有 ,从而
,从而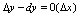 所以
所以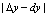 是
是 时关于
时关于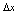 的高阶无穷小,即
的高阶无穷小,即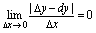 .这说明:当
.这说明:当 很微小时,
很微小时,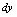 是
是 的近似值,即
的近似值,即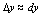 .2.可微与可导的关系[定理1]
.2.可微与可导的关系[定理1] 在点
在点 处可微的充分必要条件是
处可微的充分必要条件是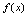 在点
在点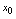 处可导.可微与可导是等价概念.由此定理的证明过程还给出如下关系式:
处可导.可微与可导是等价概念.由此定理的证明过程还给出如下关系式: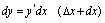 即
即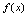 在一点的微分等于
在一点的微分等于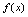 在该点的导数乘自变量的微分.3.微分的几何意义
在该点的导数乘自变量的微分.3.微分的几何意义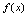 在点
在点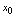 处的微分
处的微分 表示曲线
表示曲线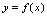 在点
在点 处的切线上横坐标为
处的切线上横坐标为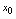 与横坐标为
与横坐标为 的两个点的纵坐标之差.(图3-1)
的两个点的纵坐标之差.(图3-1)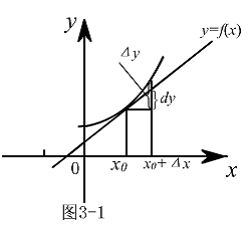
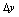 是曲线上两点纵坐标之差,由图3-1可看出,当
是曲线上两点纵坐标之差,由图3-1可看出,当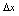 越微小时,
越微小时,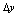 与
与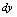 之差就越小,所以
之差就越小,所以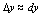 对微小的
对微小的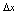 有效.二、微分法则1.基本微分公式由于可微与可导是等价概念,且由
有效.二、微分法则1.基本微分公式由于可微与可导是等价概念,且由 ,可知有如下基本微公公式.
,可知有如下基本微公公式.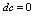 (
( 是常数)
是常数) (
(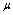 为实数)
为实数)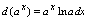 ,
,
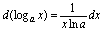 ,
,
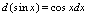
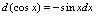

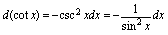
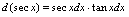
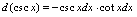
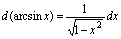

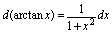
 2.微分四则运算法则设
2.微分四则运算法则设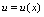 ,
, ,
,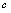 是常数,则
是常数,则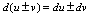


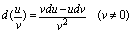 3.复合函数微分法(微分形式不变性)
3.复合函数微分法(微分形式不变性)