第五章 不定积分
学习目的和要求
本章主要学习和了解原函数和不定积分的概念,不定积分的基本公式,不定积分换元积分法和分部积分法.
具体要求如下:
1.理解原函数与不定积分的概念.掌握不定积分的基本性质.
2.熟练掌握不定积分的基本公式.
3.熟练掌握不定积分的第一类换元法,掌握不定积分的第二类换元法(仅限于三角代换与简单的根式代换).
4.熟练掌握不定积分的分部积分法.
本章主要内容
第一节 不定积分概念
一、原函数〈定义5.1〉设在区间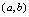 有
有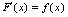 或
或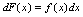 则称
则称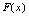 是
是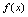 在
在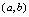 内的原函数.二、不定积分定义〈定义5.2〉函数
内的原函数.二、不定积分定义〈定义5.2〉函数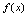 的全体原函数称为
的全体原函数称为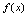 的不定积分,记为
的不定积分,记为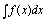 三、不定积分的几何意义由不定积分定义,若
三、不定积分的几何意义由不定积分定义,若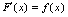 , 则
, 则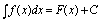
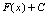 为无穷多条曲线,通常称为
为无穷多条曲线,通常称为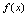 的积分曲线族。由
的积分曲线族。由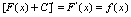 可知,在点
可知,在点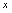 处,积分曲线族中每条曲线有相同的导数,按导数的几何意义,由相同的切线斜率,即切线平行,于是有:
处,积分曲线族中每条曲线有相同的导数,按导数的几何意义,由相同的切线斜率,即切线平行,于是有: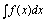 表示一族曲线,族中每条曲线在点x处有平行的切线.
表示一族曲线,族中每条曲线在点x处有平行的切线.
第二节 不定积分的运算性质
性质1、不定积分与微分(求导数)互为逆运算.性质2、代数和的积分等于积分的代数和.性质3、常数因子可以提到积分号外.
第三节 基本积分公式与直接积分法
一、基本积分公式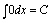 (C是常数)
(C是常数)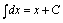
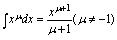 (常用结果:
(常用结果: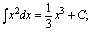
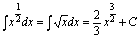 等)
等)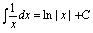
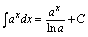
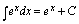
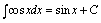
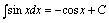
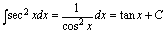
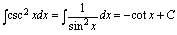
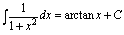
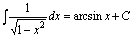 二、直接积分法利用不定积分的性质和积分基本公式计算不定积分的方法就是直接积分法.
二、直接积分法利用不定积分的性质和积分基本公式计算不定积分的方法就是直接积分法.
第四节 换元积分法
一、第一换元积分法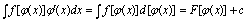 二、第二换元积分法1、三角换元
二、第二换元积分法1、三角换元
第五节 分部积分法
一、分部积分法由微分公式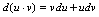 两边求不定积分
两边求不定积分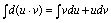 根据不定积分性质
根据不定积分性质 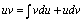 变形,得:
变形,得: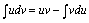 此式即为分部积分公式。第六节 附记不定积分的结果的初等表达式可以不唯一.
此式即为分部积分公式。第六节 附记不定积分的结果的初等表达式可以不唯一.