题型: 单项选择题
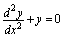 的通解的是( )
的通解的是( )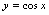
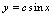 (
(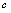 是任意常数)
是任意常数)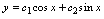 (
(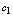 ,
,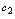 是任意常数)
是任意常数)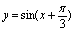
首先验证是否是解,再判明是否通解.根据解的概念,只须将及其导数代入方程,若方程两端恒等,则可判明是解. 对A,,,,代入方程. 对B,,,,代入方程. 对C,,,,代入方程, 对D,,,,代入方程. 因此,所给函数都是方程的解.由于方程是二阶微分方程,只有中含两个任意常数,所以中函数是通解.
题型: 解答题
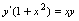 的通解.
的通解.分离变量,有: 两边积分 所以,所求方程通解为:(是任意常数).
求解微分方程时,一般应首先判断方程的类型,然后用相应的解法求解,将此方程变形: , 判明此方程为可分离变量方程. 关于微分方程的解法 要求掌握以下三类一阶微分方程的解法. (1)变量可分离方程,解法是:分离变量,两边积分即得通解. (2)齐次微次方程,解法是:用齐次代换化方程为可分离变量方程,求出的通解后再将代回. (3)一阶线性微分方程: 一阶线性齐次微分方程的通解公式为 一阶线性非齐次微分方程的通解公式为 通过计算积分可求出通解. 若求满足初始条件的特解,应先求出通解,将初始条件代入通解,确定任意常数的值,将值代入通解即得满足初始条件的特解.
题型: 解答题
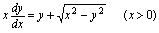 的通解.
的通解.将方程化为 令,则,,代入原方程: 分离变量,得: 两边积分, 从而,将代回,故所求微分方程的通解为:
分析:方程两边除以,得 由此可知该方程为齐次微分方程.
题型: 解答题
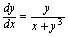 满足初始
满足初始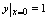 的特解.
的特解.将方程改写为:,其中, 所以 即方程的通解为: 初初始条件代入通解式: 故方程满足初始条件的特解为:
此方程中变量,不可分离,又关于,也不是齐次多项式,不构成齐次方程,又微分方程也不是关于未知函数的一阶线性微分方程,但方程两边取倒数,有: 可改写为: 这是以为未知函数的一阶线性非齐次方程,其中 ,