第三章 导数与微分
题目1
题型: 单项选择题
例1.设
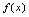 在点
在点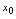 处可导,则
处可导,则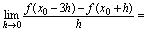 ( )
( )A.
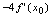
B.

C.
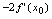
D.
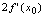
答案:
应选A.
分析:
这里表示自变量增量,为使被求极限式符合导数的定义式,则应对分子变形: 于是 上式等号右端的第二项已符合导数的定义式,应等于,第一项尚不符合定义域,还应变形: 故结果为 本题目依据导数定义解答: 导数定义如下: 或 左导数 右导数存在存在且相等.
题目2
题型: 单项选择题
例2.设
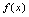 在
在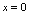 处可导,
处可导,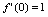 ,且
,且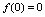 ,则
,则 ( )
( )A.0
B.1
C.
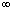
D.不可确定
答案:
应选B.
分析:
已知,由定义有,根据已知,故可将改写为,所以.
题目3
题型: 解答题
例3.求曲线
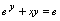 上点
上点 处的切线方程和法线方程.
处的切线方程和法线方程.答案:
将代入,有:,从而切点坐标为. 对两边求导:,将代入,知. 故切线方程为:,即 法线方程为:,即
分析:
此类型题目思路如下. 导数的几何意义及应用. 给出曲线上点处曲线切线的斜率. 曲线上点(此点即为切点)处的切线方程为: 法线方程为: 关于切线(法线)方程的建立,有如下两类问题. (1)已知切点横坐标.求解步骤为:将代入,计算切点纵坐标;求出,然后写出切线(法线)方程. (2)已知某点处切线与已知直线的位置关系,(平行或垂直).求解步骤为:设切点.根据切点在曲线上,可得方程;求出,按已知条件建立切线斜率应满足的等式,即又一个方程,解此方程组,得,进而写出切线(法线)方程.
题目4
题型: 解答题
例4.求曲线
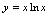 的平行于直线
的平行于直线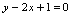 的切线方程.
的切线方程.答案:
设切点为. ,点处的切线斜率为. 又,已知直线,,斜率为2,由题设,两直线平行,斜率相等,从而,,知,再由,知,所以切点为,. 故所求切线方程为:,即
分析:
此类型题目思路如下. 导数的几何意义及应用. 给出曲线上点处曲线切线的斜率. 曲线上点(此点即为切点)处的切线方程为: 法线方程为: 关于切线(法线)方程的建立,有如下两类问题. (1)已知切点横坐标.求解步骤为:将代入,计算切点纵坐标;求出,然后写出切线(法线)方程. (2)已知某点处切线与已知直线的位置关系,(平行或垂直).求解步骤为:设切点.根据切点在曲线上,可得方程;求出,按已知条件建立切线斜率应满足的等式,即又一个方程,解此方程组,得,进而写出切线(法线)方程.
题目5
题型: 解答题
例5.设
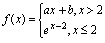 ,当
,当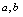 为何值时,
为何值时,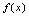 在
在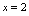 可导.
可导.答案:
解: 因此,得, 从而,再由,有 综上,可知,时,在处可导.
分析:
分析:在可导,应满足,在可导,则在必连续,应满足. 关于函数在一点处可导与连续的关系. 若设在点可导,则在点连续.根据可导的充要条件是左、右导数存在且相等;连续的必要条件是极限存在,即左、右极限存在且相等,可列举两个等式(即两个方程),由此可解常见的如下问题.