第六章 定积分
题目1
题型: 单项选择题
例1.下列定积分值为正值的是( )
A.
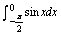
B.
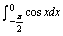
C.
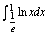
D.
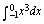
题目2
题型: 单项选择题
例2.下列不等式中,正确的是( )
A.
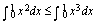
B.
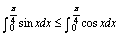
C.
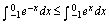
D.
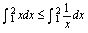
题目3
题型: 单项选择题
例3.设
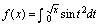 ,则
,则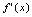 =( )
=( )A.

B.
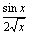
C.
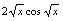
D.
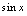
题目4
题型: 单项选择题
例4.设
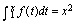 ,则
,则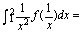 ( )
( )A.
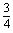
B.
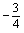
C.3
D.-3
题目5
题型: 解答题
例5.讨论
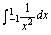 如何计算
如何计算题目6
题型: 单项选择题
例6.
 ( )
( )A.2
B.3
C.
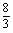
D.
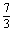
题目7
题型: 解答题
例7.求
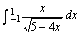
题目8
题型: 解答题
例8.求曲线
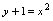 与直线
与直线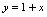 所围图形的面积.
所围图形的面积.题目9
题型: 解答题
例9.求由曲线
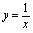 ,
,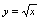 与直线
与直线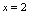 所围图形绕
所围图形绕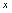 轴旋转一周生成的旋转体的体积.
轴旋转一周生成的旋转体的体积.