第五章 不定积分
题目1
题型： 解答题
例1．
，
，
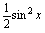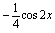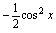是同一个函数的原函数吗？答案：
解：根据原函数定义，只要它们的导数是同一个函数，它们就都是那个函数的原函数．
分析：
这说明所给三个函数都是同一个函数的原函数．即一个函数的原函数的初等函数表达式是可以完全不同的法则． 由于 这又说明了，即使同一个函数的原函数的初等表达式的法则不同，但彼此之间也仅相差一个常数，正因为如此，所以可以用一个原函数加任意常数表示全体原函数． 不定积分概念：的全体原函数为的不定积分．根据不定积分这样的定义，不定积分的结果的初等函数表达式不是唯一的． 由例1、知： 这三个等式都是成立的．
题目2
题型： 单项选择题
例2．下列等式中，正确的是（ ）
A．
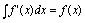
B．
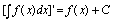
C．
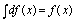
D．
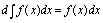
答案：
选D．
分析：
只须按性质1审定，、中由于后进行不定积分计算，故都应加，故不正确．中由于后进行求导数运算，不应加，故不正确． 不定积分性质． 应重点理解透彻性质1，即不定积分与微分（求导）互为逆运算，这种关系，可由四个关系式表出： ，，
题目3
题型： 单项选择题
例3．
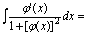（ ）A．
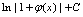
B．
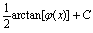
C．
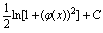
D．
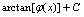
答案：
选D
分析：
被积函数含这个复合函数表达式，具有符合积分公式的格式，所以想到将改写为，由于被积函数恰含，而可写为，故待求积分，以为积分变量符合公式的格式，于是，有： 关于不定积分的基本积分公式与第一换元法． 应熟记基本积分公式，同时，应理解积分公式的格式不变性．如公式可表为 亦可表为． 但在时， 即，被积函数法则下的变量和后的变量相同时应认为符合公式，若变量不同，则不可认为符合公式，这就是所谓积分公式的格式不变性． 第一换元积分法（凑微分法）的实质，就是改变积分变量的表达式，使积分符合公式的格式． 若待求积分为，被积函数含复合函数与内层法则的导数因子，由于，从而，当法则符合公式且由公式可知的原函数法则为的话，则，这里将积分变量换为,使待求积分符合公式的格式是求积分的关键．将写出就是所谓的凑微分．
题目4
题型： 解答题
例4．求
答案：
<法一>由于，即 ，所以 <法二>
分析：
法二中，经二次凑微分，先将凑成，然后再以为变量，将凑成，这类同于将凑成． 常用的凑微分的结果如下： 或或或或或 等等．
题目5
题型： 解答题
例5．计算
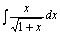
答案：
解：<法一>分项，凑微分 <法二>根式代换 令 <法三>分部积分法 此外，还可令或令求解．
分析：
不定积分的方法具有多样性，灵活性特点，应通过做题积累经验，不断提高计算能力．