第四章 微分中值定理与导数应用
题目1
题型： 单项选择题
例1．函数
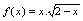在
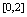上满足罗尔定理的
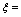（ ）A．1
B．
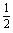
C．
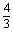
D．
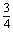
答案：
选
分析：
罗尔定理的结论是，所以应令解得其在内的根即为． 令，由 得，故．
题目2
题型： 单项选择题
例2．函数
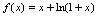在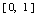
满足拉格朗日定理的
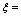( )．A．
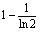
B．
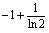
C．
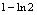
D．
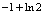
答案：
选．
分析：
拉格朗日定理的结论是，所以令，其根若在内，即为． ，， 由 ，，， 所以
题目3
题型： 解答题
例3．计算
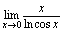
答案：
=
分析：
时，分子，分母，对式用洛必达法则计算．
题目4
题型： 解答题
例4．计算
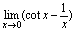
答案：
分子、分母同除以
分析：
当时，，，对式通分化比式后，用洛必达法则计算
题目5
题型： 解答题
例5．求函数
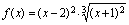在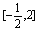
上的最大值与最小值．答案：
令，得内部的驻点，又在处不存在，但不在内，舍去，不予讨论． 因为 ，，，所以，．
分析：
一般说来，连续函数在上的最大值与最小值，可以由区间端点函数值与区间内及不存在的点的函数值相比较，其中最大的就是函数在上的最大值，最小的就是函数在上的最小值．
题目6
题型： 解答题
例6．设扇形的周长为常量
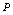，问：当扇形的半径为何值时，使扇形的面积最大？答案：
设扇形的半径为，弧长为，用s 表示扇形面积，根据几何学知识，有： 且 由（2）,，（3）代入（1）得； ，令，得驻点，又，，所以在处 取唯一极大值． 答：当扇形半径为时，可使扇形面积最大．
分析：
此题属于极值的应用问题．