第二章 极限与连续
题目1
题型： 解答题
例1．求
．答案：
= = =1
分析：
当时，；，分子、分母均为关于的整式，则因式分解，约去，再用商的法则求解．
题目2
题型： 解答题
例2．求
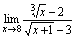
答案：
= = = = =
分析：
当时，；，分子、分母为含根式的无理式，则应互乘共轭根式，约去，再用商的法则求极限．
题目3
题型： 解答题
例3．设
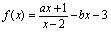，在
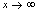过程中，当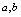
满足什么条件时，
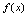是无穷大？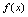
是无穷小？
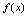以2为极限？答案：
是无穷大，应有，即 = = 根据上述结论，分子次数应高于分母次数，因此分子应含项，所以，可含也可不含项，所以可为任意实数． 当，为任意实数时，在时是无穷大． 同理，为无穷小，应满足分子次数低于分母的次数，即满足，所以，当，时，在时是无穷小． 以2为极限，要求分子，分母同为一次多项式，且一次项系数之比为2，即满足且，所以当时，在时以2为极限．
分析：
关于（或）时分式的极限． 讨论极限，这里分子是关于的次多项式，是常数系数；分母是关于的次多项式，是常数系数． 求解的思路是：分子、分母同时除以的最高次幂，为中较大者，结论是：
题目4
题型： 解答题
例4．求
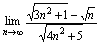
答案：
分子、分母同时除以，有 = = = =
分析：
分析：在时，无理分式的极限的运算，类同于上述有理分式极限计算的思路：分子、分母同时除以的最高次幂．
题目5
题型： 单选题
例5．单项选择题：当
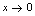时，下列无穷小中与
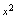为同阶非等价的无穷小的是（ ）A．
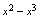
B．
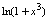
C．
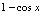
D．
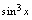
答案：
选
分析：
，当时，与 等价，不选． ，当时，比高阶，不选． = = 所以选． ，不选．
题目6
题型： 解答题
例6．求
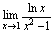
答案：
= = = =
分析：
分析：当时，；，又当时，，而，故，应用无穷小代换．
题目7
题型： 解答题
例7．讨论极限
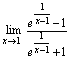
答案：
=为未定式，故分子配项，变形． = =1 = = 由于右、左极限不相等，故所讨论极限不存在．
分析：
解此例的要点是：当时，由于，所以．从而；当时，由于，所以，从而．因此，应讨论处的左，右极限，再根据函数在一点处极限存在的充要条件作出结论．
题目8
题型： 解答题
例8．求
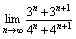
答案：
= =
分析：
此例中时， 关于指数函数在时的极限问题． 约定，则；，若，由于，则，所以；． 如：；；
题目9
题型： 解答题
例9．求
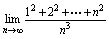
答案：
= = = =
分析：
分析：此类问题属数列极限，表示项数，在时，分子为无穷多项的和，所以不可认为 只有写出由表达的通式，才有利于求出极限． 此例中用到的通式是：= 关于无穷多项代数和的极限计算常用的通式有： （1） （2）设，当时，由于，所以．
题目10
题型： 解答题
例10．求
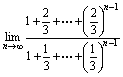
答案：
= = = =2
分析：
此类问题中，另一种情况是：写不出项和的通式，则可根据准则，即夹逼定理讨论极限．
题目11
题型： 解答题
例11．求
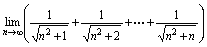
答案：
由于写不出通式，故用如下途径计算，将各项分母均改写，构造项和 = 将各项分母均改写为，构建项和 记= 由于从中的第二项开始，各项的分母大于，从而各项小于，即知 由于从中的第2项开始，各项的分母小于，从而各项大于，即知 又 由，知．
分析：
写不出项和的通式，则可根据准则，即夹逼定理讨论极限．
题目12
题型： 解答题
例12．设
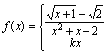
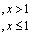当
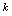为何值时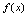
在定义域连续．答案：
定义域为 在内，有定义，连续． 在内有定义，连续． 在处 = 当时，，，从而在处连续，综上可知，当时，在定义域连续．
分析：
关于分段函数连续性的判定问题 分段函数连续性的判定应分为两种情况讨论， （1）在自变量的某取值区间内，归结为初等函数，只要有定义，则必定连续． （2）在自变量分段点处，应依据定义，通过讨论是否满足 来判定．而确定存在，又往往归结为讨论左、右极限．