第七章 多元函数微积分
题目1
题型: 解答题
例1.设
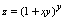 ,求
,求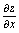 ,
,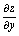
答案:
解:由于出现在底式中,对求偏导数时,应看作常数,对来说构成幂函数,所以应按幂函数求导. 由于出现在底式和指数中,对求导时,应按幂指函数求导. 对两边取对数, 两边对求导, 所以
分析:
此例说明,对指定的自变量求偏导数时,二元函数解析式关于该自变量构成哪类函数,是正确选择求导公式或法则的基础.
题目2
题型: 解答题
例2.设
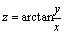 ,求
,求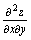
答案:
分析:
混合偏导数为第一次对求偏导数,第二次再对求偏导数.
题目3
题型: 解答题
例3.设
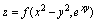 ,求
,求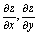
答案:
分析:
分析:设,,则,函数为二中间变量二自变量复合函数,求偏导数所用公式可用如下线路图表示. 关于二元复合函数微分法. 二元复合函数有如下三种类型: (1)两中间变量两自变量,即 (2)一个中间变量,两自变量,即 (3)两中间变量,一个自变量,即 二元复合函数对自变量的导数计算公式分别为: (1) (2) (3)
题目4
题型: 解答题
例4.设
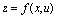 ,
,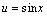 ,求
,求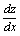
答案:
由求对的导数时,若记为易与待求的混淆,所以通常记为.
分析:
题设函数为二中间变量一个自变量的二元复合函数,中的应视为中间变量,求导线路图如下:
题目5
题型: 解答题
例5.求
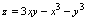 的极值
的极值答案:
, 令 由①,代入②,有,,得,;当时,;当时,,驻点为,. 又,, 在处,由于,所以在处函数无极值. 在处,由于且,所以在处函数取极大值.
分析:
此题为关于二元函数的极值问题. 设,方程组的解称为驻点,驻点是极值点的必要点. 令,, 判定极值的充分条件是: (1)当时,无极值. (2)当时,在取极值. 时,是极小值. 时,是极大值. (3)当时,不能判定.
题目6
题型: 解答题
例6.计算
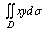 ,其中
,其中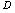 是由
是由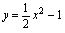 和
和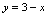 所围平面区域.
所围平面区域.答案:
<法一>将D投影到轴,则, <法二>将D投影到轴,在A、C两点之间,左边界曲线为,右边界为直线和,故应用BE将D分割为上、下两个子区域. 上方区域为 下方区域为 (投影到轴时,先对积分,应将看作自变量,为因变量,故由解反函数,其中为左半支,为右半支;由解反函数). 说明:带*的积分为零的理由是:积分计算时,是常数,是关于的奇函数,积分上、下限恰为一对相反数,所以积分值为零,零再对求定积分仍为零. 此例启发我们认识到,将二重积分化为二次积分时,应注意选择积分次序,以使计算简便.解此例时,法一优于法二.
分析:
分析:为确定积分限,首先应作的图形,而为作图形,又应解出包围的各曲线的交点,根据图形会有利于确定积分限. 由,得,,,,由此解得,. 当,时,由可计算得,,从而交点为,. 的图形见图7-1阴影部分.