当前位置：课程讲解 > 2章 > 3节 > 3点
第三节无穷小量与无穷大量
三、无穷小量的运算性质
三、无穷小量的运算性质[定理1]设
，
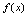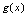是同一过程中的无穷小量，则
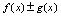仍是该过程中的无穷小量.[定理2]设
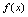是某过程中的无穷小量，
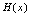是有界函数，则
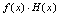仍是该过程中的无穷小量.<推论1>常数乘无穷小量仍是无穷小量.<推论2>有极限的函数乘无穷小量仍是无穷小量.<推论3>无穷小量乘无穷小量仍是无穷小量.<推论4>无穷小量的有限次幂仍是无穷小量.例1．计算
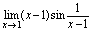解：当
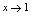时，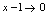
，
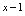是无穷小量.当
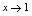时，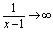
，
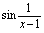振荡无极限，但
，它是有界量.根据定理2，当
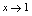时，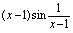
是无穷小量，所以
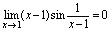.例2．计算
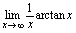解：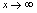
，
，
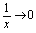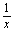是无穷小量.当
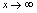时，
没有极限，但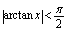
，它是有界量.根据定理2，当
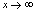时
是无穷小量，所以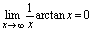
.由于无穷小量收敛于0的快慢（即趋向于的速度）并不是总一样的，所以无穷小量的商是变化趋势不定的变量.若设
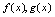是同过程中的无穷小量，则称
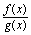是未定式，由于无穷小量以0为极限，所以两个无穷小量的比式在形式上可记为
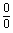.由无穷小量的运算性质与无穷小量和无穷大量的关系，可有如下结论：设
，
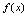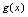是同一过程中的无穷大量，则
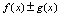是未定式.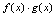
是无穷大量.
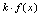是无穷大量（
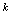是常数，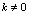
）
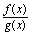是未定式，形式是可记为
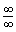.如：
，
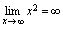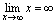，而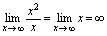
，
，
.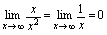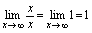