当前位置:课程讲解 > 1章 > 3节 > 3点
第三节函数的几种简单性质
三、函数的单调性
三、函数的单调性<定义1.5>设函数
 在
在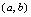 内有定义,任取
内有定义,任取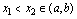 1.如果
1.如果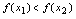 ,则称
,则称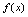 在
在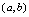 单调增加,简称单调增,区间
单调增加,简称单调增,区间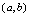 称为
称为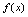 的单调增区间.2.如果
的单调增区间.2.如果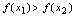 ,则称
,则称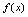 在
在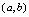 单调减少,简称单调减,区间
单调减少,简称单调减,区间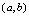 称为
称为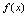 的单调减区间.在单调增区间,函数图形是沿
的单调减区间.在单调增区间,函数图形是沿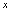 轴正向的上升曲线(见图1-6或图1-7).
轴正向的上升曲线(见图1-6或图1-7).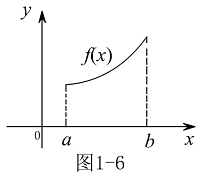
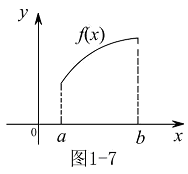 在单调减区间,函数图形是沿
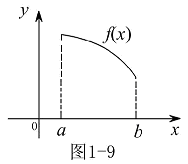
在单调减区间,函数图形是沿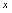 轴正向的下降曲线(见图1-8或图1-9).
轴正向的下降曲线(见图1-8或图1-9).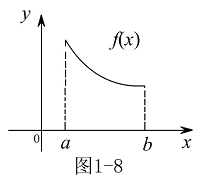
 <定义1.6>若函数
<定义1.6>若函数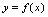 在定义域
在定义域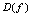 只有一种单调性(单调增或单调减),则称
只有一种单调性(单调增或单调减),则称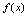 为单调函数.如函数
为单调函数.如函数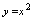 ,其定义域为
,其定义域为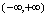 ,由其图形(见图1-10)可知,在
,由其图形(见图1-10)可知,在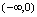 单调减,在
单调减,在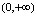 单调增,它不是单调函数.
单调增,它不是单调函数.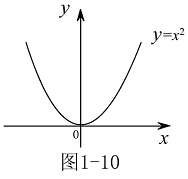 再如函数
再如函数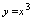 ,其定义域为
,其定义域为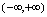 ,由其图形(见图1-11),可知,在
,由其图形(见图1-11),可知,在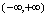 单调增,它是单调函数且是单调增函数.
单调增,它是单调函数且是单调增函数.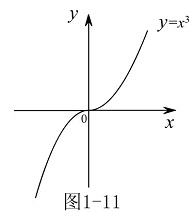 简单情况下,可根据函数的图形的上升或下降判明单调增减性.复杂情况下,以后将建立判定条件.
简单情况下,可根据函数的图形的上升或下降判明单调增减性.复杂情况下,以后将建立判定条件.