当前位置:课程讲解 > 1章 > 1节 > 1点
第一节预备知识
一、绝对值
一、绝对值1.绝对值概念<定义1.1>实数
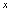 的绝对值记为
的绝对值记为 ,规定为
,规定为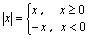
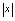 的几何意义是:
的几何意义是: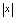 表示数轴上的点
表示数轴上的点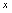 (在原点左边或右边)与原点之间的距离.2.有关绝对值的运算性质(1)
(在原点左边或右边)与原点之间的距离.2.有关绝对值的运算性质(1)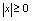 (2)
(2)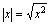 (3)
(3)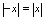 (4)
(4) (5)
(5)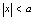 与
与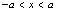 等价,即:
等价,即: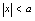 则
则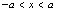 ;
;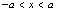 则
则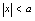 .(这里
.(这里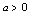 )(6)
)(6)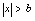 与
与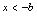 或
或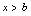 等价.(这里
等价.(这里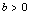 )(7)
)(7)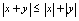 (8)
(8)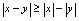 (9)
(9)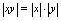 (10)
(10)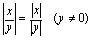 例1.化简下式:
例1.化简下式: 分析:因分子含
分析:因分子含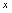 的绝对值,应按
的绝对值,应按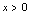 或
或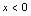 两种情况讨论.解:当
两种情况讨论.解:当 时,
时,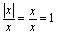 ;当
;当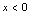 时,
时,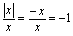 .例2.解下列不等式(1)
.例2.解下列不等式(1)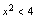 (2)
(2)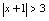 (3)
(3)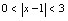 (4)
(4)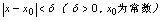 分析:(1)为解出
分析:(1)为解出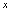 ,等式两边开平方,根据性质(2),
,等式两边开平方,根据性质(2),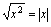 ,容易出错为
,容易出错为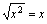 .(2)根据性质(6)可解.(3)因为
.(2)根据性质(6)可解.(3)因为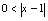 ,可知
,可知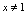 ,这一点容易被忽略.(4)应习惯用字母
,这一点容易被忽略.(4)应习惯用字母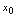 表示常数,即
表示常数,即 为已知的某个实数.解:(1)
为已知的某个实数.解:(1)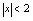 ,所以
,所以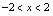 .(2)
.(2)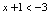 且
且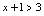 ,即
,即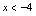 或
或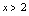 .(3)
.(3)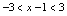 且
且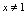 ,所以
,所以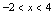 且
且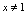 .
.(4)
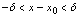 ,
,