当前位置:课程讲解 > 1章 > 3节 > 1点
第三节函数的几种简单性质
一、函数的奇偶性
一、函数的奇偶性<定义1.3>给定函数
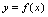 ,其定义域为
,其定义域为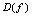 (
(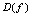 不止一个零点)(1)如果对一切
不止一个零点)(1)如果对一切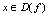 ,满足
,满足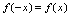 ,则称
,则称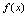 为偶函数.(2)如果对一切
为偶函数.(2)如果对一切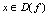 ,满足
,满足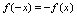 ,则称
,则称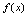 为奇函数.(3)如果对一切
为奇函数.(3)如果对一切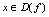 ,既不满足
,既不满足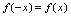 ,也不满足
,也不满足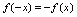 ,则称
,则称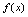 为非奇非偶函数.对偶函数,由于
为非奇非偶函数.对偶函数,由于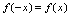 ,如果点
,如果点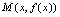 在
在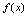 图形上,则点
图形上,则点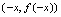 即点
即点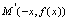 也必在
也必在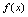 图形上,所以偶函数的图形关于
图形上,所以偶函数的图形关于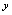 轴轴对称。(如图1-4)
轴轴对称。(如图1-4)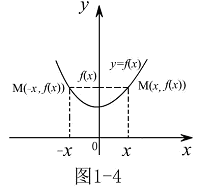 对奇函数,由于
对奇函数,由于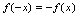 ,如果点
,如果点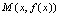 在
在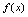 图形上,则点
图形上,则点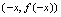 即点
即点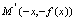 也必在
也必在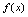 图形上,所以奇函数的图形关于坐标原点中心对称.(如图1-5)
图形上,所以奇函数的图形关于坐标原点中心对称.(如图1-5)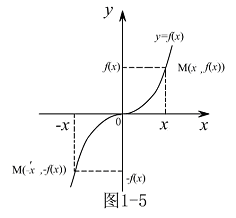 非奇非偶函数的图形无对称.由定义可知,关于函数
非奇非偶函数的图形无对称.由定义可知,关于函数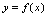 的奇偶性的判定,归结为讨论
的奇偶性的判定,归结为讨论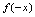 与
与 的关系例1.判定函数
的关系例1.判定函数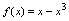 的奇偶性.解:
的奇偶性.解: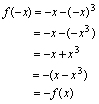 所以
所以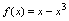 是奇函数.例2.判定函数
是奇函数.例2.判定函数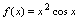 的奇偶性.解:
的奇偶性.解: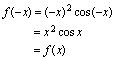 所以
所以 是偶函数.例3.判定函数
是偶函数.例3.判定函数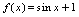 的奇偶性.解:
的奇偶性.解: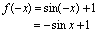 所以
所以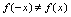 ,而
,而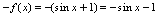 ,从而
,从而 ,故
,故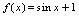 是非奇非偶函数.例4.设
是非奇非偶函数.例4.设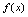 在
在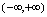 有定义,试证
有定义,试证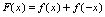 是偶函数.证:
是偶函数.证: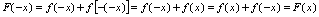 所以
所以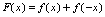 是偶函数.仿此例,可证
是偶函数.仿此例,可证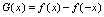 是奇函数.例5.设
是奇函数.例5.设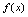 为偶函数,
为偶函数,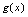 为奇函数,试证
为奇函数,试证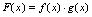 为奇函数.证:
为奇函数.证: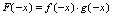 已知
已知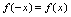 ,
,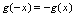 所以
所以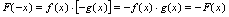 ,故
,故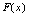 为奇函数.仿此,可证下述结论正确.(1)偶函数之和为偶函数;奇函数之和为奇函数;偶函数与奇函数之和非奇非偶.(2)偶函数之积为偶函数;奇函数之积为偶函数;偶函数乘奇函数为奇函数.常遇到的函数中,
为奇函数.仿此,可证下述结论正确.(1)偶函数之和为偶函数;奇函数之和为奇函数;偶函数与奇函数之和非奇非偶.(2)偶函数之积为偶函数;奇函数之积为偶函数;偶函数乘奇函数为奇函数.常遇到的函数中, (
(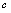 是常数),
是常数),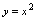 ,
,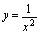 ,
,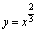 ,
,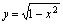 ,
,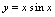 ,
,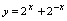 等是偶函数;
等是偶函数;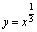 ,
, ,
,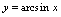 ,
,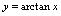 ,
,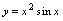 ,
,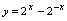 等是奇函数.
等是奇函数.