高等数学

第二节函数概念

二、函数表示法

    
    1．函数的三种表示法
    （1）解析式法
    用含自变量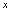的式子表示函数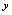的方法是解析式法。含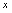的式子叫函数的解析表达式。如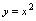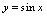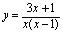：，，等等。
    特别地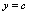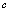（是常数）称为常数函数，意义是无论自变量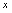取何实数值，对应的函数值都是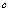，常数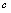是其解析表达式。
    （2）表格法
    将自变量取值与对应的函数值列成表格，用此种方法表示函数的方法就是表格法。如下表就是正弦函数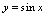当自变量取若干特殊值时的表格法。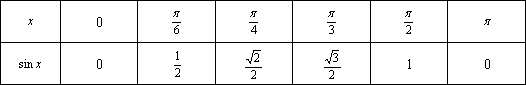
    

    
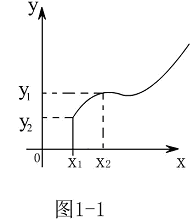
    　　（3）图形法
    在函数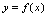中，以自变量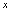的取值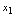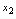，，……为点的横坐标，以与之对应的函数值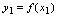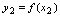，……为点的纵坐标，可在平面直角坐标系下标出点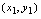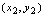，……，依自变量从小到大的次序用光滑曲线连续点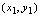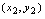，……所得平面曲线叫函数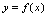的图形。用曲线表示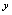与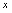的函数关系的方法就是图形法。（见图1-1）
    

    
    实际中，三种方法可结合使用，尤其以解析法和图形法结合使用的时候更多。
    2．分段函数
    如果一个函数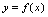，对定义域中自变量不同的值，不能用一个统一的解析式表示函数的对应法则，必须用两个或更多的解析式表示，则称这个函数为分段函数。
    如：
    

    

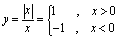
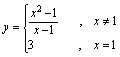
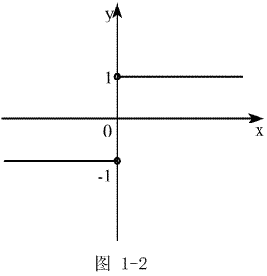
    都是分段函数，它们的图形分别见图1-2和图1-3。
    

    

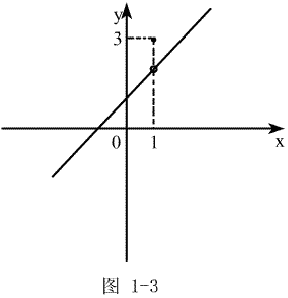
    分段函数是由两个或以上解析式表示的一个函数，不是多个函数。
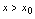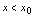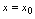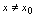    在分段函数中，如果与时表示对应法则的解析式不同，或与时表示对应法则的解析式不同，则称点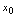为分段点。如上述两分段函数中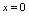，和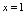就是分段点。
    3．隐函数
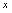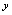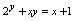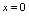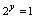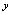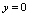    设有含，的二元方程，令，代入方程，得，解此只令的方程，得；令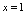，代入方程，得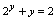，解此只含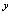的方程（虽然现在不知如何求解），假定其解为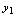，按此程序做下去，对于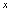的每个取值，通过方程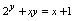总有唯一确定的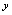值与之对应，故可认为因变量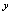是先决取值的自变量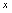的函数。但这个函数关系无法表示为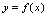的形式。这里，我们称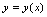是由二元方程所决定的隐函数。
    相对隐函数，能表示为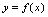的函数，如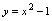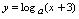，等等，称为显函数。
    由于显函数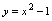总可以变形为二元方程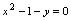，所以显函数可看作能解出因变量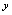的隐函数，但隐函数不能看作都是可解出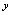的显函数。