当前位置:课程讲解 > 1章 > 2节 > 1点
第二节函数概念
一、函数定义
<定义1.2>若
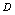 是一个非空实数集合,
是一个非空实数集合,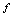 表示某种对应规则,若对每一个
表示某种对应规则,若对每一个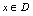 ,在规则
,在规则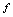 总有一个唯一确定的实数
总有一个唯一确定的实数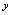 与之对应,则称对应规则
与之对应,则称对应规则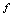 为定义在
为定义在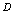 上的一个函数关系,或称变量
上的一个函数关系,或称变量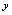 是变量
是变量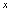 的函数,记作
的函数,记作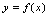 .
.称为自变量,
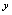 称为因变量.
称为因变量.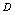 称为函数
称为函数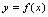 的定义域,通常记为
的定义域,通常记为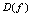 .
.当
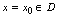 时,对应的函数值记为
时,对应的函数值记为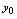 或
或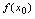 或
或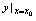 .
.当
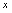 取遍
取遍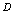 中一切值时,所对应的函数值的集合称为函数的值域,记作
中一切值时,所对应的函数值的集合称为函数的值域,记作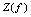 .
.关于函数定义应注意以下概念要点:
1.定义域和对应规则(即运算规则)是构成函数关系的两个要素.在定义域相同,而对应规则不同时,函数的值域必定不同,所以对应规则可由值域体现.
2.在具体问题中,
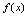 表示含
表示含 的运算式,称为函数的解析表达式,如:
的运算式,称为函数的解析表达式,如: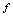 的内容为“二次幂运算”,则
的内容为“二次幂运算”,则 可表示
可表示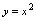 ,这里
,这里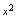 是函数的解析表达式.由此应理解,既使不写成方程
是函数的解析表达式.由此应理解,既使不写成方程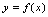 的形式,只写出
的形式,只写出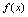 即可表式成一个函数,即
即可表式成一个函数,即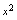 ,
,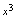 ,
,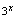 ,
,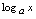 ,
,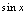 ,
, 等等均表示自变量的函数,特别地,
等等均表示自变量的函数,特别地,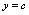 (
(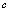 是常数)亦表示一个函数,通常称为常数函数.
是常数)亦表示一个函数,通常称为常数函数.3.函数定义域不能是空集.如果对任何实数
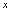 按给定的对应规则找不到与之相应的
按给定的对应规则找不到与之相应的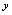 值,当然应该认为对应规则
值,当然应该认为对应规则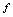 是无意义的,所以不能认为
是无意义的,所以不能认为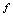 是函数关系.如:设
是函数关系.如:设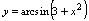 .当
.当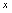 取任意实数
取任意实数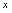 时,总有
时,总有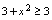 ,而
,而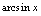 要求
要求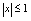 时有意义,故知规则
时有意义,故知规则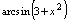 对任意实数
对任意实数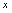 均无意义,所以
均无意义,所以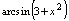 不是
不是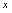 的函数.
的函数.4.因变量值应是唯一确定的.若在对应规则
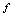 下,对每一个
下,对每一个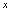 值有不止一个因变量
值有不止一个因变量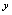 值与之对应,则不可认为
值与之对应,则不可认为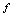 决定了一个函数.如
决定了一个函数.如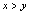 ,对于一个
,对于一个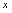 值,有无穷多个
值,有无穷多个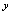 值与之对应,由“>”体现的对应规则不可认为确定了一个函数.再如由方程
值与之对应,由“>”体现的对应规则不可认为确定了一个函数.再如由方程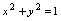 解出
解出 时得
时得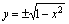 ,对于一个
,对于一个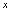 值,有两个
值,有两个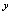 值与之对应,故不可认为由方程
值与之对应,故不可认为由方程 体现的对应规则确定了一个函数.
体现的对应规则确定了一个函数.例1.确定函数的定义域
(1)
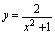
(2)
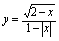
(3)
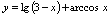
分析:依定义域的概念,即使对应规则(运算规则)有意义的自变量取值集合,决定了确定函数定义域的方法是,按运算规则列举含
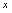 的不等式(组),不等式(组)的解的集合给出定义域.通常用区间形式表示定义域.常见运算规则有以下4种:分母不为零;偶次根式被开方式非负(即大于等于零);对数真数大于零;
的不等式(组),不等式(组)的解的集合给出定义域.通常用区间形式表示定义域.常见运算规则有以下4种:分母不为零;偶次根式被开方式非负(即大于等于零);对数真数大于零; 及
及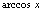 要求
要求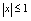 .
.解:
(1)对任何实数
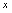 有
有 ,所以.
,所以.(2)
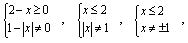 所以
所以(3)
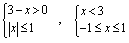 所以
所以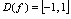
例2.设函数
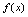 的定义域为
的定义域为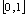 ,则
,则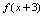 的定义域是___.
的定义域是___.填
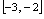
分析:根据定义域概念,当
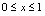 时,对应规则
时,对应规则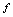 有意义,故对
有意义,故对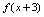 应满足
应满足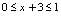 .由此可解出
.由此可解出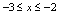 .
.例3.下列各组函数中,表示相同函数的是( ).
A.
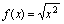 与
与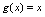
B.
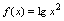 与
与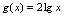
C.
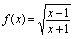 与
与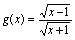
D.
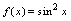 与
与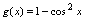
应选D.
分析:根据函数概念,函数两要素是定义域和对应法则,而对应法则由值域体现,所以,当且仅当定义域和值域完全相同时,才可认为两个函数是相同函数.
A中,两函数的定义域都是
 ,但值域不同,
,但值域不同, 的值域为
的值域为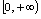 ,
, 的值域为
的值域为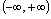 .
.B中,两函数的定义域不同,
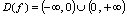 ,
,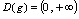 .
.C中,两函数的定义域不同,
 ,
,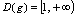 .
.D中,两函数的定义域同为
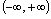 ,值域同为
,值域同为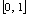 .
.例4.已知
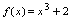 ,求
,求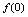 ,
,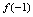 ,
,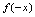 ,
,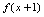 ,
,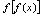 .
.分析:由函数概念所求均为函数
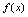 在自变量
在自变量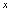 取定值点对应的函数值,用自变量取定值替换函数表达式中的
取定值点对应的函数值,用自变量取定值替换函数表达式中的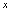 ,经计算或化简即得所求.
,经计算或化简即得所求.解:
例5.已经
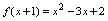 ,求
,求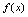 .
.分析:参照例4所求
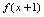 可知,已知
可知,已知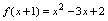 可理解为在
可理解为在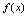 中,当
中,当 取
取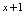 时所得结果.若将等式右端的
时所得结果.若将等式右端的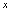 化为
化为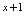 ,再将
,再将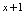 代之以
代之以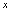 ,则可得
,则可得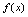 的表达式,为将
的表达式,为将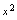 表为
表为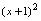 ,注意到
,注意到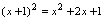 ,故应构造出
,故应构造出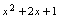 ,可配成
,可配成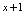 的平方.
的平方.解:
方法一
所以
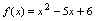 方法二
方法二令
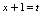 ,则
,则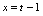 ,一并代入已知,有
,一并代入已知,有即