当前位置:课程讲解 > 1章 > 4节 > 1点
第四节反函数、复合函数
一、反函数
一、反函数<定义1.8>设
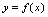 的定义域为
的定义域为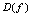 ,值域为
,值域为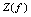 .如果对于每一个
.如果对于每一个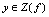 都有一个确定的满足
都有一个确定的满足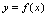 的
的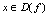 与之对应,其对应规则记为
与之对应,其对应规则记为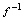 (读作
(读作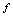 逆),这个定义在
逆),这个定义在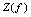 上的函数
上的函数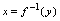 称为
称为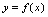 的反函数(原型反函数).亦称
的反函数(原型反函数).亦称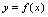 与
与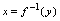 互为反函数.一对函数互为反函数的概念的本质是:互为逆法则,可参见图1-12理解.
互为反函数.一对函数互为反函数的概念的本质是:互为逆法则,可参见图1-12理解.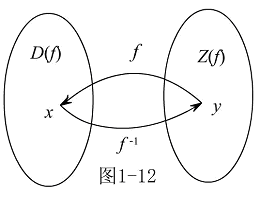 在
在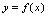 中,
中,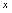 是自变量,
是自变量,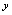 是因变量,定义域为
是因变量,定义域为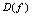 ,值域为
,值域为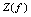 .在
.在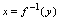 ,
,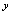 是自变量,
是自变量,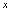 是因变量,定义域为
是因变量,定义域为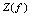 ,值域为
,值域为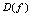 .由此可知,求已给函数的反函数就是从方程
.由此可知,求已给函数的反函数就是从方程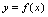 解
解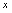 ,即用含
,即用含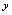 的解析式表示
的解析式表示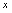 .由于我们习惯用
.由于我们习惯用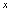 表示自变量,用
表示自变量,用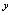 表示因变量,因此通常将
表示因变量,因此通常将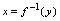 改写为
改写为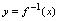 ,并称
,并称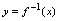 是
是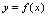 的反函数(矫型反函数),求
的反函数(矫型反函数),求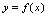 的反函数要求最终表为矫型反函数.由反函数的定义可知,
的反函数要求最终表为矫型反函数.由反函数的定义可知,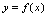 的定义域是
的定义域是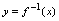 的值域,
的值域,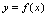 的值域是
的值域是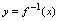 的定义域.由于
的定义域.由于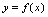 与
与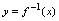 的关系的本质是
的关系的本质是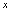 与
与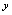 互换,即平面上点的横纵坐标互换,所以
互换,即平面上点的横纵坐标互换,所以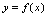 的图形与
的图形与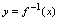 的图形关于直线
的图形关于直线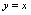 轴对称.例1.求函数
轴对称.例1.求函数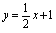 的反函数.解:由
的反函数.解:由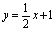 解
解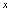 :
: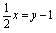 ,
,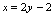 故所求为
故所求为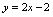 由图1-13可看出两直线关于
由图1-13可看出两直线关于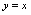 轴对称.
轴对称.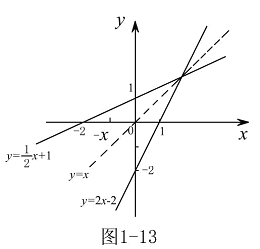 例2.设
例2.设 ,又
,又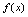 与
与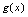 的图形关于
的图形关于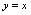 对称,求
对称,求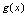 的解析式.解:由一对反函数的图形的对称关系,可知
的解析式.解:由一对反函数的图形的对称关系,可知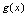 应为
应为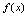 的反函数,故由
的反函数,故由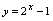 解
解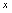 即可得
即可得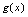 .
.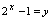 ,
,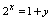 ,
,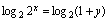 ,
,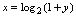 ,所以
,所以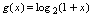 .
.