当前位置:课程讲解 > 1章 > 4节 > 2点
第四节反函数、复合函数
二、复合函数
二、复合函数<定义1.9>设函数
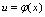 ,值域为
,值域为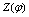 ,函数
,函数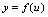 ,定义域为
,定义域为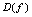 ,如果
,如果 与
与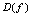 的交集
的交集 不是空集,则称
不是空集,则称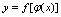 ,是由
,是由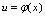 与
与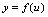 复合而得的复合函数.
复合而得的复合函数.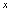 是自变量,
是自变量, 是因变量,
是因变量,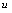 是中间变量.例1.写出
是中间变量.例1.写出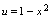 ,
,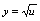 复合而得的复合函数.解:用
复合而得的复合函数.解:用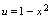 替换
替换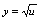 中的
中的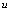 ,得
,得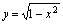 ,因为
,因为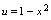 的值域是
的值域是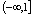 ,
,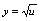 的定义域是
的定义域是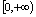 ,而其交集
,而其交集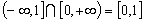 不是空集,所以
不是空集,所以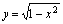 是复合函数.例2.写出
是复合函数.例2.写出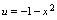 ,
,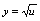 复合而得的复合函数.解:用
复合而得的复合函数.解:用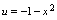 替换
替换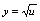 中的
中的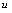 ,得
,得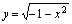 ,因为
,因为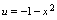 的值域是
的值域是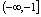 ,
,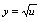 的定义域是
的定义域是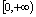 ,而其交集
,而其交集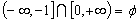 ,所以
,所以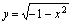 对任何实数
对任何实数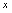 无定义,故
无定义,故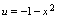 ,
,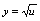 不可复合得复合函数.例3.函数
不可复合得复合函数.例3.函数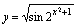 可看作是由
可看作是由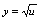 ,
,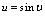 ,
,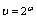 ,
,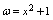 复合而得的复合函数.将一个复杂的函数看作由若干个简单函数复合而得的复合函数,有利于对函数的研究.因此,这是一个很重要的基本能力.
复合而得的复合函数.将一个复杂的函数看作由若干个简单函数复合而得的复合函数,有利于对函数的研究.因此,这是一个很重要的基本能力.