第三节函数的几种简单性质
四、函数的有界性
四、函数的有界性<定义1.7>设函数
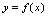
在区间
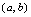
有定义,以任意
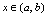
,如果存在正数
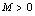
,使得
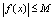
,则称
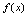
在
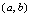
有界,区间
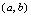
称为
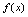
的有界区间.如果满足上述不等式的
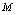
不存在,则称
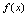
在
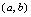
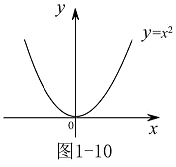
无界.对简单函数,可根据函数图形是否分布在有限范围判明其有界性,而对较复杂的函数不要求讨论.如:函数
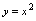
,根据图形(图1-10)可知它在
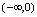
无界,在
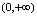
无界,而在
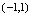
有界.
应重点掌握下述函数的有界性.函数
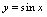
,定义域为
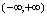
,由于对任意
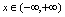
,恒有
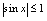
,所以
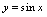
在定义域
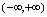
有界.同理,由于对任意实数
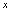
,恒有
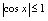
,所以
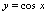
在定义域
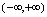
有界.事实上,
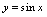
,
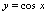
的图形都是夹在水平直线
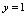
与
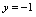
之间的波形曲线.